GEB
Duglas R. Hofshtadter.
[ predydushchaya ] [ oglavlenie ] [ sleduyushchaya ]

Perevod Aleksandra Semenova

G L A V A   I
MU-golovolomka

Formal'naya Sistema

Central'nym ponyatiem etoj knigi yavlyaetsya formal'naya sistema. Formal'naya sistema, kotoruyu ya budu dalee ispol'zovat', byla izobretena v 20-h godah amerikanskim logikom |milem Postom, i ee chasto nazyvayut "porozhdayushchaya sistema Posta". |ta glava poznakomit vas s etoj formal'noj sistemoj i, krome togo, ya ochen' nadeyus', u vas vozniknet zhelanie hot' nemnogo ee issledovat'. Poetomu dlya razzhiganiya vashego interesa ya izlozhu nebol'shuyu zagadku.

Zagadka v sleduyushchem: "Mozhete li vy poluchit' MU?"* Dlya nachala vy budete snabzheny cepochkoj simvolov. CHtoby ne derzhat' vas v temnote, skazhu srazu, chto eto cepochka simvolov - MI. Dalee budut raz®yasneny nekotorye pravila, po kotorym vy mozhete zamenyat' odnu cepochku simvolov na druguyu. Esli odno iz etih pravil primenimo k vybrannoj cepochke, i vy hotite ego primenit', to mozhete eto sdelat'. No net nichego takogo, chto by vam diktovala kakoe konkretno pravilo nado primenyat', esli vy okazhetes' na rasput'e, i vam pridetsya vyborom iz neskol'kih odinakovo dopustimyh variantov. |tot vybor ostaetsya za vami. I konechno etot vybor prevrashchaet ogranichennuyu formal'nymi ramkami igru v nechto pohozhee na iskusstvo.

Glavnyj moment, kotoryj pochti ne nuzhdaetsya v ob®yasnenii, eto to, chto vy ne dolzhny delat' chego-libo, chto ne ogovoreno v pravilah. My mogli by nazvat' eto ogranichenie "Trebovaniem Formal'nosti". V glave s nazvaniem "Formal'naya sistema", navernoe, eto "pravilo" vryad li stoilo podcherkivat' osobo. Odnako, hotya eto zvuchit stranno, ya predskazyvayu, chto kak tol'ko vy nachnete igrat' s predlozhennoj zdes' sistemoj, vy narushite Trebovanie Formal'nosti mnogo raz, esli, konechno, vy ne rabotali s formal'nymi sistemami prezhde.

* V etoj knige, my budem priderzhivat'sya sleduyushchego soglasheniya, kogda obrashchaem vashe vnimanie na cepochki simvolov. Esli cepochki pishutsya tak, chto ih tyazhelo otlichit' ot teksta predlozheniya, to oni budut vzyaty v edinichnye ili dvojnye kavychki. Punktuaciya, kotoraya prinadlezhit predlozheniyu, a ne cepochke, budet idti za predelami kavychek, kak eto diktuet logika. Naprimer, pervaya bukva etogo predlozheniya - N, v to vremya kak pervaya bukva ' etogo predlozheniya. ' - ' e '. Odnako, kavychki budut obychno opuskat'sya, esli vse yasno i bez nih. Naprimer, pervaya litera kvadrata - k.

Pervoe, chto sleduet skazat' o nashej formal'noj sisteme, MIU-sisteme, sostoit v tom, chto ona ispol'zuet vsego tri bukvy latinskogo alfavita: M, I i U (eti tri bukvy tak i nazyvayut: a l f a v i t sistemy -prim. A.S). |to znachit, chto cepochki simvolov v MIU-sisteme - eto tol'ko te cepochki, kotorye sostavlennye iz etih treh bukv. Vot nekotorye primery takih cepochek:

    MU
    UIM
    MUUMUU
    UIIUMIUUIMUIIUMIUUIMUIIU

I hotya vse eti cepochki vpolne dopustimy, oni ne yavlyayutsya temi cepochkami, kotorye "nahodyatsya v vashej vlasti" ili "sobstvennosti". Fakticheski, edinstvennaya poka prinadlezhashchaya vam cepochka- cepochka MI. I tol'ko ispol'zuya pravila, kotorye sejchas budut predstavleny, vy mozhete popolnit' vashu sobstvennuyu kollekciyu novymi cepochkami.
Vot pervoe pravilo:

    Pravilo I: Esli vy imeete cepochku simvolov, poslednij simvol kotoroj - I, vy mozhete pribavit' k nej v konec simvol U.

Otmechu, mezhdu prochim (esli vy do etogo momenta ne zadumyvalis' o znachenii termina "cepochka"), chto cepochka predpolagaet, raspolozhenie simvolov v opredelennom poryadke. Naprimer, MI i IM - dve razlichnye cepochki. Uchtite, eto ne prosto "meshochek" s simvolov, v kotoryj te svaleny kuchej, i ih poryadok ne imeet znacheniya.

Teper' vtoroe pravilo:

    Pravilo II: Predpolozhim, chto vy imeete Mx, togda vy mozhete dobavlyat' Mxx k vashej kollekcii.

CHto pod etim podrazumevaetsya, ya pokazhu na primerah nizhe:

Iz MIU, vy mozhete poluchit' MIUIU.
Iz MUM, vy mozhete poluchit' MUMUM.
Iz MU, vy mozhete poluchit' MUU.

Litera 'x' v pravile stavitsya vmesto lyuboj podcepochki simvolov. No kak tol'ko vy reshite, kakaya eto podcepochka, vy dolzhny chetko priderzhivat'sya etogo vybora (poka vy ne ispol'zuete eto pravilo v sleduyushchij raz, gde vy budete delat' novyj vybor). Obratite vnimanie na tretij iz privedennyh vyshe primerov. On pokazyvaet kak vy, odnazhdy poluchiv MU, mozhete poluchat' iz nee druguyu cepochku simvolov dlya popolneniya vashej kollekcii. No prezhde vy nepremenno dolzhny poluchit' MU!
YA hochu dobavit' poslednij kommentarij otnositel'no simvola 'x'. |tot simvol ne yavlyaetsya chast'yu formal'noj sistemy, takim zhe, kak litery M, I i U. No, tem ne menee, on polezen nam, ibo pozvolyaet govorit' o podcepochkah simvolov voobshche. Zadacha simvola 'x' - stoyat' za proizvol'nuyu posledovatel'nost' simvolov v preobrazuemoj cepochke. No esli vy kogda-nibud' dobavite k vashej kollekcii cepochku, soderzhashchuyu sam simvol 'x' , to vy sdelaet chto-to nepravil'no. Potomu chto cepochki MIU-sistemy nikogda ne soderzhat simvol 'x'.
Imeetsya tret'e pravilo.

    Pravilo III: Esli podcepochka III vstrechaetsya v kakoj-libo cepochke vashej kollekcii, to vy mozhete poluchit' novuyu cepochku podstavlyaya simvol U na mesto III.
Naprimer:

    Iz UMIIIMU, vy mozhete poluchit' UMUMU.
    Iz MIIII, vy mozhete poluchit' MIU (ili MUI).
    Iz IIMII, vy ne mozhete nichego poluchit', ispol'zuya eto pravilo. (Tri I dolzhny stoyat' posledovatel'no)
    Iz MIII, poluchaetsya MU.
YA ochen' nadeyus', chto vas ne posetit ideya primenyat' eto pravilo v obratnuyu storonu. Naprimer, tak:

Iz MU, poluchaetsya MIII. < = |to neverno!

Vse pravila odnostoronnie.
Nakonec imeetsya poslednee pravilo.

    Pravilo IV: Esli podcepochka UU vstrechaetsya vnutri odnoj iz vashih cepochek, vy mozhete isklyuchit' ee.
Iz UUU, poluchitsya U.
Iz MUUUIII poluchitsya MUIII

Teper' my imeem vse, chto nam neobhodimo, i vy mozhete poprobovat' poluchit' MU. Ne volnujtes', esli vy ne dostignite uspeha. Prosto poprobujte nemnogo. Glavnoe dlya vas sejchas - pochuvstvovat' vkus MU-golovolomki.

Teoremy, Aksiomy, Pravila

Otvet na MU-golovolomku poyavit'sya v knige pozzhe. Poka vazhno ne najti otvet, a sam poisk otveta. Vy, nadeyus', sdelali neskol'ko popytok poluchit' MU. Sovershaya eti popytki, vy poluchili sobstvennuyu kollekciyu cepochek. Takie cepochki simvolov, poluchaemye po pravilam, nazyvayutsya teoremami. Konechno, termin "teorema" obychno primenyaetsya v matematike, kotoraya ves'ma otlichaetsya ottogo, chto my tut vystroili. "Teorema" - eto utverzhdenie na obychnom yazyke, istinnost' kotorogo dokazyvaetsya strogim logicheskim sposobom, tipa Teoremy Zenona otnositel'no "ne sushchestvovaniya" dvizheniya, ili Teoremy Evklida o beskonechnosti mnozhestva prostyh chisel. No v formal'nyh sistemah o teoremah nel'zya dumat' kak ob utverzhdeniyah. Zdes' teoremy- cepochki simvolov. Vmesto togo, chto by byt' samodostatochnymi istinami, nashi teoremy kak budto proizvedeny mashinoj, soglasno nekotorym tipografskim pravilam. CHtoby v dal'nejshem podcherkivat' eto vazhnoe razlichie v znacheniyah termina "teorema", ya v etoj knige primu sleduyushchee soglashenie: kogda "teorema" pishetsya s zaglavnoj bukvy, ee znachenie budet kazhdodnevnym. Teorema - utverzhdenie na obychnom yazyke, kotoroe kto-to, kogda-to dokazal kak istinnoe utverzhdenie s pomoshch'yu strogih argumentov. Esli zhe "teorema" pishetsya s malen'koj bukvy, to imeetsya v vidu tehnicheskoe znachenie: eto cepochka simvolov, poluchennaya mehanicheski v nekotoroj formal'noj sisteme. V etom smysle MU-golovolomka zvuchit tak: yavlyaetsya li MU teoremoj MIU-sistemy?
Dlya togo, chto by s chego-to mozhno bylo nachat', ya dal vam odnu "svobodnuyu" cepochku, a imenno MI. Takaya svobodnaya teorema nazyvaetsya aksiomoj - termin, tehnicheskoe znachenie kotorogo zdes', tak zhe ves'ma dalek ot obshcheizvestnogo. Formal'naya sistema mozhet imet' nol', odnu, neskol'ko ili dazhe beskonechnoe chislo aksiom. Primery vsego etogo my eshche vstretim na protyazhenii nashej knige.
Kazhdaya formal'naya sistema imeet pravila dlya soedineniya simvolov tipa vysheprivedennyh chetyreh pravil MIU-sistemy. Oni nazyvayutsya ili pravilami dokazatel'stva ili pravilami vyvoda. YA budu ispol'zovat' oba termina.

I poslednij termin, kotoryj ya hochu predstavit' v etom razdele - vyvod.
Nizhe pokazano, kak vyvedena teorema MUIIU:

(1) MI ........................... Aksioma
(2) MII .......................... Iz (1) v sootvetstvii s pravilom II
(3) MIIII ....................... Iz (2) v sootvetstvii s pravilom II
(4) MIIIIU .................... Iz (3) v sootvetstvii s pravilom I
(5) MUIU ...................... Iz (4) v sootvetstvii s pravilom III
(6) MUIUUIU ............... Iz (5) v sootvetstvii s pravilom II
(7) MUIIU ..................... Iz (6) v sootvetstvii s pravilom IV

Vyvod teoremy pokazyvaet yavno, shag za shagom, kak poluchaetsya iskomaya teorema iz aksiomy soglasno pravilam formal'noj sistemy. Ponyatie vyvoda identichno ponyatiyu dokazatel'stva, no vyvod - nam poka kazhetsya tol'ko blizhajshim bratom dokazatel'stva. Ved' zvuchalo by stranno, chto vy dokazali MUIIU, no ne stol' stranno zvuchit, chto vy vyveli MUIIU.

Vnutri i snaruzhi Sistemy

Bol'shinstvo lyudej, pristupiv k resheniyu MU-golovolomki, proizvodyat naugad mnozhestvo teorem tol'ko dlya togo, chto by posmotret', chto iz etogo poluchit'sya. Dovol'no skoro oni nachinayut zamechat' nekotorye svojstva teh cepochek, kotorye poluchili. |to to, chto chelovecheskij intellekt obychno shvatyvaet mgnovenno. Naprimer, vozmozhno, eto srazu ne bylo ochevidnym, chto vse teoremy sistemy nachinayutsya s simvola M. No vskore vy uvideli eto na mnozhestve primerov. So vremenem oboznachilas' obshchaya zakonomernost' i malo togo, chto vy mogli zametit' ee, vy mogli ponyat' ee spravedlivost'. Priglyadevshis' k pravilam, vy mogli soobrazit', chto kazhdaya novaya teorema nasleduet pervuyu bukvu ot bolee rannej teoremy. V itoge poluchaetsya, chto pervyj simvol vseh teorem byli unasledovany ot pervogo simvola edinstvennoj aksiomy MI i eto dokazyvaet, chto vse teoremy MIU-sistemy dolzhny nachinat'sya s simvola M.

Iz vsego etogo voznikaet vazhnyj vyvod. Vysheskazannoe demonstriruet odno razlichie mezhdu lyud'mi i mashinami. U nas est' vozmozhnost' postroit' (fakticheski eto ochen' legko sdelat') komp'yuternuyu programmu, kotoraya by nepreryvno stroila teoremy MIU-sistemy, i my mogli by vklyuchit' v programmu komandu, kotoraya by ostanavlivala process tol'ko posle togo, kak budet poluchena stroka U. Teper' vy znaete, chto komp'yuter, tak zaprogrammirovannyj, nikogda ne ostanovitsya. I eto vas ne udivlyaet. No chto budet, esli vy poprosite druga poluchit' U? Vas niskol'ko ne udivit, esli drug cherez nekotoroe vremya vernetsya i zayavit vam, chto net nikakogo sposoba izbavit'sya ot simvola M v nachale vseh cepochek i poetomu reshat' vashu zadachu - chto vodu v stupe toloch'. Dazhe esli chelovek ne ochen' soobrazitelen, on vse ravno ne mozhet ostavit' bez vnimaniya podozritel'nuyu zakonomernost' i, v konce koncov, u nego nakopitsya intuitivnoe nedoverie k zadache - eto ta intuiciya, kotoroj komp'yuternoj programme, kak my ee opisali, ne hvataet.
Teper' pozvol'te mne bolee tochno ob®yasnit', chto ya imel v vidu govorya, mol, pokazhu raznicu mezhdu chelovekom i mashinoj. YA polagayu vpolne vozmozhnym, chtoby programmiruemaya mashina vypolnyala rutinnuyu zadachu takim sposobom, chto ona nikogda ne budet zamechat' dazhe ochevidnye fakty otnositel'no, togo, chto delaet, no eto nevozmozhno dlya chelovecheskogo soznaniya - ne zamechat' nekotorye fakty otnositel'no togo, chto on delaet. Vy eto prekrasno ponimaete. Esli vy naberete na klavishah schetnoj mashinki "1", a potom pribavlyaete k etomu 1, i zatem pribavite 1 snova, snova i snova, i tak budete prodolzhat' v techenii mnogih chasov, to schetnyj mehanizm nikogda ne nauchitsya povtoryat' vashi dejstviya i delat' etu operaciyu uzhe neposredstvenno bez vas, hotya lyuboj chelovek priobrel by podobnyj mehanicheskij navyk ochen' bystro. Ili, voz'mem glupyj primer. Avtomobil' nikogda ne priobretet sobstvennyh navykov (ne zavisimo ot togo, kak horosho i kak dolgo ego vodili) dlya togo, chtoby izbegat' drugie avtomobilyami ili prepyatstviyami na doroge, i on nikogda ne obuchitsya samostoyatel'no ezdit' dazhe po tem marshrutam, gde ochen' chasto ezdili vmeste s hozyainom.
Korennoe razlichie v tom, chto dejstvovat' sovershenno bez vnimaniya - dlya mashiny vpolne vozmozhno, no sovershenno nevozmozhno dlya cheloveka. Zamete, ya ne govoryu, chto vse mashiny obyazatel'no ne sposobny k glubokim nablyudeniyam. Net, tol'ko nekotorye mashin. I pri etom ya ne govoryu, chto vse lyudi vsegda delayut tonkie nablyudeniya. Lyudi, kak pravilo, ochen' chasto okazyvayutsya vopiyushche nevnimatel'nymi. No mashiny mogut byt' sdelany tak, chto by dejstvovat' absolyutno nevnimatel'no, a lyudi na takoe ne sposobny. I poka bol'shaya chast' mashin, hotya vyglyadyat oni dovol'no simpatichno, sdelany sovershenno nevnimatel'nymi. Veroyatno po etoj prichine, dlya bol'shinstva lyudej, svojstvo byt' nevnimatel'nym, kazhetsya harakternoj osobennost'yu mashin. Naprimer, esli kto-to govorit, chto nekotoraya zadacha "mehanicheskaya", to eto ne znachit, chto lyudi ne sposobny ee vypolnit', eto znachit, chto tol'ko mehanizm mog by vypolnyat' etu rutinu mnogo raz podryad bez zhalob i chuvstva skuki.

Skachek iz Sistemy

Takoe obychno svojstvenno intellektu - vzyat' da i vyprygnut' iz zadachi, kotoruyu on pytaetsya reshit', poiskat' reshenie snaruzhi, so storony. I chasto takoj vzglyad izvne prinosit rezul'taty. YA skazal, chto intellekt mozhet vyprygnut' za predely reshaemoj zadachi, no eto ne znachit, chto tak byvaet vsegda. Odnako malejshee pobuzhdenie k etomu, kak pravilo, okazyvaetsya mgnovenno udovletvoreno. Naprimer, cheloveka chitayushchego knigu, mozhet smorit' son. Togda vmesto togo, chtoby uporno prodolzhat' chitat' do konca, on, po vsej vidimosti, otlozhit knigu i vyklyuchit svet. Tem samym on sdelaet shag "iz sistemy" i etot vyhod vyglyadit vpolne estestvenno v nashem mire. Ili, predpolozhim, persona A smotrit televizor, kogda persona V vhodit v komnatu i demonstriruet svoe neudovol'stvie situaciej. Persona A polagaya, chto pravil'no ponimaet sut' pretenzij V, nachinaet v ramkah sushchestvuyushchej sisteme pytat'sya uluchshit' situaciyu: manipuliruya knopkami kanalov, iskat' luchshuyu programmu. No persona V mozhet imet' bolee radikal'nuyu koncepciyu, kotoraya lezhit "za predelami sistemy", a imenno - vyklyuchit' televizor voobshche!
Inogda sluchaetsya tak, chto kakoj-libo chelovek uvidit kontury sistemy, vliyayushchej na sud'by mnogih lyudej. On vidit sistemu, kotoruyu ran'she dazhe nikogda ne priznavalas' kak sistema. Togda etot chelovek poroj vynuzhden tratit' svoyu zhizn', daby ubedit' drugih v tom, chto sistema dejstvitel'no sushchestvuet, nuzhno tol'ko vyjti iz nee, chto by uvidet' ochevidnoe!

Kak zhe nauchit' komp'yutery vyprygivat' iz sistemy? YA privedu primer, kotoryj udivil nekotoryh nablyudatelej. Nedavno, na shahmatnom turnire v Kanade, odna shahmatnaya programma (i eto byla naislabejshaya iz vseh predstavlennyh tam programm) prodemonstrirovala neobychnuyu maneru zakanchivat' igru zadolgo do final'nogo hoda. Programma ne byla ochen' horoshim shahmatistom, no etot nedostatok s lihvoj okupalsya ee sposobnost'yu svoevremenno opredelit', chto igra nahodit'sya v beznadezhnoj situacii i poetomu pora sdavat'sya, ne dozhidayas' poka sopernik ispolnit dlitel'nyj ritual naneseniya okonchatel'nogo porazheniya. Programma proigrala vse partii. No ona ih vse proigrala ochen' stil'no! Na mnogih mestnyh ekspertov po shahmatam eto proizvelo neizgladimoe vpechatlenie!
Takim obrazom, esli vy opredelite "sistemu" kak "sovershat' shagi v shahmatnoj igre", yasno, chto eta programma imela horoshuyu sposobnost' k vyhodu iz sistemy. S drugoj storony, esli vy dumaete o vyhode iz "sisteme" kak o dejstvii, "kotoroe ne bylo zaprogrammirovan zaranee", togda, bez somneniya, komp'yuter ne imeet voobshche nikakoj vozmozhnosti vyjti iz sistemy.

Ochen' vazhno pri izuchenii formal'nyh sistem otlichit' rabotu v predelah sistemy ot zaklyucheniya utverzhdenij ili nablyudenij otnositel'no samoj sistemy. YA polagayu, chto vy, nachav reshat' MU-golovolomku, kak i bol'shinstvo lyudej, rabotali v predelah sistemy, no potom v vas nachalo rasti bespokojstvo i eto bespokojstvo, v konce koncov, dostiglo toj tochki, gde vy prekratili dal'nejshie popytki dobit'sya rezul'tata. Vy vyshli iz sistemy, poprobovali ocenit' uzhe sdelannoe vami, i zadalis' voprosom - pochemu do sih por tak i ne smogli poluchit' MU? Vozmozhno, vy nashli prichinu pochemu ne smogli poluchit MU. Pri etom vy uzhe dumali otnositel'no vsej sistemy v celom. Vozmozhno, vy poluchili MIII, gde-libo v processe raboty, i etot rezul'tat vy mogli poluchit', tol'ko rabotaya vnutri sistemy. YA ne stal by utverzhdat', chto eti dva sposoba polnost'yu nesovmestimy. YA uveren, chto kazhdyj chelovek sposoben do nekotoroj stepeni rabotat' vnutri sistemy i odnovremenno razmyshlyat' otnositel'no togo, chto on delaet. Fakticheski, pri reshenii real'nyh problem, pochti nevozmozhno provesti granicu mezhdu tem, chto nahodit'sya "vnutri sistemy" i "snaruzhi". ZHizn' sostoit iz takogo kolichestva vzaimnyh svyazej i hitrospletenij, chasto soderzhit stol'ko protivorechivyh "sistem", chto mozhet pokazat'sya slishkom uproshchennym dumat' o nej v takih terminah. No chasto okazyvaetsya ochen' vazhnym sformulirovat' prostye i yasnye idei, daby potom ispol'zovat' ih kak modeli v razmyshleniyah otnositel'no bolee slozhnyh sushchnostej. I imenno poetomu ya demonstriruyu vam formal'nye sistemy, poetomu nam pora vernut'sya k obsuzhdeniyu MU-golovolomki.

M-sposob, I-sposob, U-sposob

MU-golovolomka byla predlozhena takim obrazom, chtoby podtolknut' vas k nekotorym samostoyatel'nym issledovanii MIU-sistemy, to est', zastavit' vas lichno poluchit' nekotoroe kolichestvo teorem. No zadacha bylo prepodnesena i tak, chto sovsem ne garantirovala voznagrazhdenie za upornyj trud tomu, kto ostanetsya vnutri sistemy. Tem samym provocirovalos' nekotoroe kolebanie v vybore mezhdu dvumya metodami raboty. Luchshij sposob razreshit' eti kolebaniya - imet' dva lista bumagi. Na odnom liste vy rabotaete "v meru svoih sposobnostej kak mashina", tem samym, zapolnyaya etot list tol'ko cepochkami simvolov iz M, I i U. Na vtorom liste vy rabotaete "v meru svoih sposobnostej kak razumnoe sushchestvo" i zdes' razreshaetsya zapisyvat' vse idei prihodyashchie vam v golovu v processe resheniya zadachi. Naprimer, vy mogli by delat' zapisi na chelovecheskom yazyke, ili predprinyat' popytku rassuzhdenij v obratnuyu storonu, pri etom vy mozhete ispol'zovat' vsevozmozhnye sokrashcheniya i special'nye simvoly (tipa simvola 'x'), szhatie neskol'kih shagov v odin. Vy mozhete probovat' pomenyat' pravila sistemy, chtoby posmotret' k chemu eto privedet, i uvidet' chto menyaetsya, a chto ostalos' neizmennym. Odna veshch', na kotoruyu vy mogli by obratit' vnimanie eto to, chto chisla 2 i 3 igrayut vazhnuyu rol', tak kak ot simvolov I mozhno izbavit'sya tol'ko imeya ih trojkami, a ot simvolov U izbavlyayutsya tol'ko dvojkami. V to zhe vremya udvoenie dlinny cepochek (ne schitaya pervogo simvola M) dopuskaetsya tol'ko pravilom II, poetomu na vashem vtorom liste vpolne mogli by poyavit'sya nekotorye soobrazheniya na etot schet...
V dal'nejshem my budem inogda vozvrashchat'sya k etim dvum sposobam obrashcheniya s formal'noj sistemoj, poetomu my nazovem ih Mehanicheskim sposobom (M-sposobom) i Intellektual'nym sposobom (I-sposobom). CHtoby zavershit' perechen' sposobov, ispol'zuya ves' alfavita MIU-sitsemy, ya tak zhe upomyanu zaklyuchitel'nyj sposob - sposob Otricaniya ili Ne-sposob (U-sposob), kotoryj yavlyaetsya Dzen-sposobom, tak skazat', priblizheniya k suti veshchej. No otnositel'no etogo sposoba my uznaem v posleduyushchih glavah.

Razreshayushchaya procedura

Nablyudaya za golovolomkoj, mozhno skazat' sleduyushchee: vse pravila razdelyayutsya na dve gruppy, kazhdaya iz kotoryh imeet protivopolozhnuyu drug drugu tendenciyu - udlinyayushchie pravila i sokrashchayushchie pravila. Dva pravila (I i II) pozvolyayut vam uvelichivat' dlinu cepochek (strogo opredelennym sposobom, konechno), dva drugih pravila pozvolyayut vam sokrashchat' dlinu cepochek (opyat' zhe zhestko predpisannym sposobom). Kazhetsya, imeetsya beschislennoe raznoobrazie vozmozhnostej, v kotoryh eti razlichnye pravila mozhno bylo by kombinirovat', i eto vselyaet nadezhdu, chto tak ili inache MU vse zhe mozhno bylo by poluchit'. Tak my mogli by poprobovat' snachala poluchit' cepochku gigantskih razmerov, a potom sokrashchat' v nej fragment za fragmentom, poka ne ostanetsya tol'ko te dva vozhdelennyh simvola. Ili (hotya eto hudshij variant) process mog by sostoyat' iz serii udlinenij, a potom ryada sokrashchenij, potom opyat' udlinenij i sokrashchenij. I tak dalee. No net nikakoj garantii, chto eto privedet k uspehu. Fakticheski, my uzhe imeli vozmozhnost' ubedit'sya, chto cepochka U ne mozhet byt' poluchena voobshche ni kakim sposobom, i kak by vy ni staralis', no v popytkah udlinyat' i sokrashchat' cepochki simvolov vy smozhete dozhdat'sya ne resheniya, a tol'ko konca sveta.

Odnako sluchaj U i sluchaj MU kazhutsya vo mnogom razlichnymi. Blagodarya ochen' prostomu kriteriyu my legko priznali poluchenie U nevozmozhnym: stroka ne nachinaetsya s simvola M (prinimaya vo vnimanie, chto vse teoremy dolzhny nachinat'sya). Ochen' udobno imet' takoj prostoj kriterij proverki ne prinadlezhnost' k mnozhestvu teorem. Odnako, kto mozhet garantirovat', chto proverka pervogo simvola pozvolyaet obnaruzhit' vse ne teoremy? Mozhet, imeetsya bol'shoe kolichestvo cepochek, kotorye nachinayutsya s M, no ih nikak nel'zya poluchit' v sisteme. Vozmozhno MU -odna iz nih. |to oznachaet, chto "pravilo pervogo simvola" imeet ogranichennye vozmozhnosti, s ego pomoshch'yu mozhno obnaruzhit' tol'ko chast' ne teorem, no ne zametit' ostal'nye. U nas zarozhdaetsya nadezhda, chto vozmozhno, sushchestvuet nekotoryj bolee slozhnyj, sposob, s pomoshch'yu kotorogo sovershenno chetko mozhno otlichit' te cepochki, chto mogut byt' polucheny v nashej sisteme, ot teh, kotorye zdes' polucheny byt' ne mogut. No tut my ostanavlivaemsya pered voprosom: "chto my podrazumevaem pod kriteriem?" Ne sovsem ochevidna prichina, pochemu etot vopros imeet smysl ili vazhen v nashem kontekste. No ya privedu primer "kriteriya", kotoryj, tak ili inache, narushaet duh nashih rassuzhdenij.
Voobrazite dzhina, vladeyushchego neogranichennym vremenem i kotoryj poluchaet udovol'stvie ot togo, chto tratit vse eto vremya na vyvod teorem MIU- sistemy, dovol'no metodichnym sposobom. Vot, naprimer, vozmozhnyj put', kotorym dzhin mog by zanimat'sya lyubimym delom:

    SHag 1: Primenit' kazhdoe primenimoe pravilo k aksiome MI. |to porodit dve novyh teoremy: MIU, MII.
    SHag 2: Primenite kazhdoe primenimoe pravilo k teoremam, proizvedennym na shage 1. |to privedet k polucheniyu treh novyh teorem: MIIU, MIUIU, MIIII.
    SHag 3: Primenite kazhdoe primenimoe pravilo ko vsem teoremam, poluchennym na shage 2. |to porodit pyat' novyh teorem: MIIIIU, MIIUIIU, MIUIUIU1U, MIIIIIIII, MUI.
*
*
*

Takim obrazom, dzhin porodit kazhduyu teoremu sistemy rano ili pozdno, potomu chto pravila primenyayutsya vo vseh myslimyh kombinaciyah. (Sm. ris. 11.) Vse sochetaniya udlinenij i sokrashchenij, kotorye my upominali vyshe, v konechnom schete, rano ili pozdno zdes' vstrechayutsya.

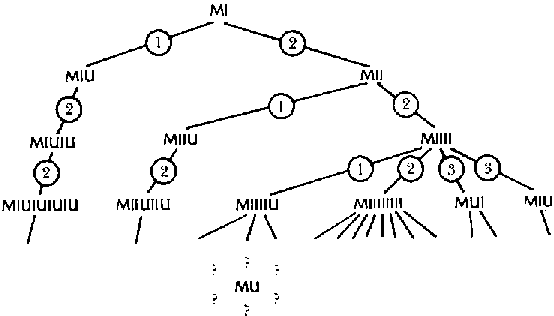
RIS. 11. Pokazano sistematicheskoe postroenie "dereva" vseh teorem MIU-SISTEMY. N-nnyj uroven' vnizu soderzhit te teoremy, proishozhdenie kotoryh trebuet tochno N shagov. CHisla v kruzhochkah soobshchayut, kakoe pravilo ispol'zovalos' na dannoj vetke dereva. Nahoditsya li MU gde-nibud' v etom dereve?

Odnako, ne sovsem yasno kak dolgo nado zhdat' poyavleniya vozhdelennoj cepochki simvolov, ved' teoremy zanesena v etot spisok v poryadke dlinny svoego proishozhdeniya. |to ne ochen' poleznyj poryadok, esli vy interesuetes' konkretnoj cepochkoj (tipa MU). I esli vy ne mozhete dazhe znat' dejstvitel'no li eta cepochka kogda-libo budet poluchena, to tem bolee ne mozhete vedat', kak mnogo shagov dlya ee vyvoda potrebuetsya! No teper' ob®yasnim predlozhennyj ranee "sposob" otlichit' teoremy ot ne teorem

    ZHdite, poka rassmatrivaemaya vami cepochka ne budet poluchena dzhinom. Kak tol'ko eto sluchit'sya vy uznaete, chto vasha cepochka - teorema. Esli zhe etogo nikogda ne sluchit'sya, znachit, rassmatrivaemaya vami cepochka - ne teorema.

Takoj podhod vyglyadit absurdnym, potomu kak po nemu predpolagaetsya, chto my ne protiv zhdat' bukval'no celuyu vechnost' dlya polucheniya neobhodimogo otveta. Zdes' my podoshli k slozhnejshej suti togo, chto my dolzhny schitat' "kriteriem". Glavnejshij priznak takogo kriteriya - garantiya, chto my poluchim ozhidaemyj otvet za konechnyj promezhutok vremeni. Poetomu esli imeetsya kriterij (sposob) proverit' lyubuyu cepochku na prinadlezhnost' k mnozhestvu teorem, kotoryj vsegda zakanchivaetsya za konechnyj promezhutok vremeni, to takoj kriterij (sposob) nazyvaetsya razreshayushchej proceduroj dlya dannoj formal'noj sistemy.
Esli vy imeete razreshayushchuyu proceduru, togda vy imeete ochen' konkretnuyu harakteristiku vseh teorem v sisteme. Po neostorozhnosti, nam moglo by pokazat'sya, chto pravila i aksiomy formal'noj sistemy obespechivayut ne menee polnuyu harakteristiku teorem, chem razreshayushchaya procedura. No vsya hitrost' v termine "harakteristika". Konechno, i pravila vyvoda, i aksioma MIU-sitemy neyavno harakterizuyut te cepochki, kotorye yavlyayutsya teoremami. Dazhe bolee togo, neyavno oni harakterizuyut te cepochki, kotorye teoremami ne yavlyayutsya. No neyavnoj harakteristiki chasto byvaet nedostatochno. Esli kto-libo utverzhdaet, chto imeet harakteristiku vseh teorem, no trebuetsya beskonechno mnogo vremeni dlya togo, chtoby vyyasnit', chto nekotorye cepochki ne teoremy, to vy, navernoe, sklonites' k mysli, chto v etoj harakteristike chego-to ne tak - ona slishkom rasplyvchata.

Imenno poetomu obnaruzhit', chto razreshayushchaya procedura sushchestvuet - ochen' vazhnyj shag. Vazhno uvidet', chto najdennoe sredstvo, v dejstvitel'nosti pozvolyaet vypolnit' ispytanie na prinadlezhnost' lyuboj cepochki k mnozhestvu teorem, i dazhe esli eto ispytanie ochen' slozhnoe, to ono vse ravno garantirovanno zakonchit'sya. V principe takoj kriterij dolzhen byt' stol' zhe legok, stol' zhe mehanichen, stol' zhe konechen i stol' zhe ubeditelen, kak proverka na nalichie pervym simvolom u vseh teorem simvola M. Razreshayushchaya procedura - lakmusovaya bumazhka dlya vseh teorem teorii!
Kstati, odnim iz trebovanij k formal'noj sisteme yavlyaetsya to, chtoby mnozhestvo aksiom harakterizovalos' razreshayushchej proceduroj. Razreshayushchaya procedura dolzhna byt' lakmusovoj bumazhkoj na "aksiomnost'". |to garantiruet, chto net nikakih problem v samom nachale, po krajnej mere, v osnovanii. V etom glavnoe razlichie mezhdu mnozhestvom aksiom i mnozhestvom teorem: aksiomy vsegda imeyut razreshayushchuyu proceduru, no teoremy mogut takoj procedury i ne imet'.
YA uveren, chto vy soglasites' so mnoj: kogda vpervye smotreli na MIU- sistemu, vy dolzhny byli videt' etu problemu otchetlivo. Edinstvennaya aksioma byla izvestna, pravila vyvoda byli prosty, tak chto teoremy byli neyavno harakterizovany. I tem ne menee vse eshche bylo ne yasno, yavlyaetsya li MU teoremoj ili net?

[ predydushchaya ][ oglavlenie ] [ sleduyushchaya ]
Sopyleft © A Semenov 2002
[ vverh ]