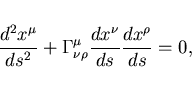 |
(1) |
Вопрос: В чем заключается усложненный вариант теории относительности?
Под усложненным вариантом, по видимому, подразумевается общая теория относительности (ОТО). Эйнштейн (A. Einstein), как известно, пытался построить общую теорию из которой бы следовали все взаимодействия, но не преуспел. Название "Общая теория относительности" принадлежит Эйнштейну. Это название является неадекватным и постепенно исчезает из литературы, заменяясь на "теорию тяготения" [1].
Построение ОТО Эйнштейн начал в 1907 году и закончил вместе Х.Д. Гильбертом (H.D Hilbert) в 1915. Большой вклад в развитие математического аппарата теории внес в 1908-10 годах Г. Минковский (H. Minkowski).
В основе ОТО лежит экспериментальный факт равенства инертной массы (входящей во 2-ой закона Ньютона) и гравитационной массы (входящей в закон тяготения) для любого тела. Это равенство проявляется в том, что движение тела в поле тяготения не зависит от его массы. Следствием этого является отсутствие гравитационно нейтральных тел.
В работе, сделанной в 1907 г., Эйнштейн предложил мысленный эксперимент [2]: представим себе гигантский небоскреб высотой 1000 км и физика, находящегося внутри свободно падающего лифта в этом небоскребе. Физик выпускает из рук платок и часы и убеждается, что они не падают на пол лифта. Если он сообщает этим вещам толчок, то они движутся равномерно и прямолинейно, пока не столкнутся со стенками лифта. Физик приходит к выводу: я нахожусь в ограниченной галилеевой системе. Условие ограниченности необходимо для того, чтобы можно было считать, что все тела испытывают одинаковое ускорение. Но физик, наблюдающий извне за падением лифта, будет судить о вещах совершенно иначе. Он видит, что лифт и все находящееся в нем движутся ускоренно в соответствии с законом тяготения Ньютона.
Этот пример показывает, что можно перейти от галилеевой системы к ускоренной, если учесть гравитационное поле. Иными словами гравитационное поле (в котором проявляется гравитационная масса) эквивалентно ускоренному движению (в котором проявляется инертная масса). Гравитационная масса и инертная масса характеризуют одно и то же свойство материи, рассматриваемое по-разному (разность массы современными экспериментальными методами не обнаружена). Таким образом, Эйнштейн пришел к принципу эквивалентности, который он так сформулировал в своей автобиографии:
В поле тяготения (малой пространственной протяженности) все происходит так, как в пространстве без тяготения, если в нем вместо "инерциальной" системы отсчета ввести систему, ускоренную относительно нее.
Данный принцип позволяет трактовать тяготение как искривление пространства-времени.
Искривление пространства-времени характеризуется символами Кристофеля.
Если все символы Кристофеля равны 0, что соответствует
отсутствию гравитационного поля, то уравнение геодезической
переходит в уравнение прямой ![]() ,
где
,
где
![]() --
ускорение тела, то есть мы получаем первый закон Ньютона.
В приближении Ньютона геодезическими линиями являются прямые.
--
ускорение тела, то есть мы получаем первый закон Ньютона.
В приближении Ньютона геодезическими линиями являются прямые.
Подробно математический аппарат и выводы следствий общей теории относительности описаны в [4].
Это выражение отличается от Ньютоновского выражения для ускорения корнем
в знаменателе. Величина ![]() стремится к бесконечности, когда
стремится к бесконечности, когда ![]() стремится
к
стремится
к
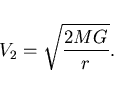 |
(4) |
Теоретическая астрофизика предсказывает возникновение черных дыр в конце эволюции массивных звезд; возможно существование черных дыр и другого происхождения (реликтовые черные дыры -- остатки после "большого взрыва"). На данный момент астрономы наблюдают объекты, которые представляют из себя двойные звездные системы, в состав которых (как предполагается) входят черные дыры.