
G L A V A IV
YAvnyj i skrytyj smysl
Vo vtoroj glave my videli kak smysl (po krajnej mere, v otnositel'no prostom kontekste formal'noj sistemy) voznikaet esli ustanovlen izomorfizm mezhdu simvolami, kotorymi manipuliruyut po pravilam, i ob容ktami real'nogo mira. CHem bolee slozhen etot izomorfizm v celom, tem bol'she nuzhno "zatratit'" usilij i sredstv, dlya izvlecheniya smysla iz simvolov. Esli izomorfizm ochen' prost (ili znakom) my sklonny govorit', chto smysl, kotoryj my vidim, - yavnyj. My vidim smysl, ne zamechaya izomorfizma. Naibolee yarkij primer etogo - chelovecheskij yazyk, gde lyudi chasto pripisyvayut smysl slovam v sebe, vmesto togo chtoby najti v samom neznachitel'nom otzvuke ochen' slozhnyj "izomorfizm", kotoryj i napolnyaet ih smyslom. |to oshibka, kotoruyu legko sdelat'. Lyudi skoree pripisyvayut priznak ob容ktam (slovam ih oboznachayushchim) chem svyazyam mezhdu etim ob容ktami i real'nym mirom. |to mozhno sravnit' s naivnoj veroj, chto shum - neobhodimyj effekt ot stolknoveniya dvuh ob容ktov. No eto- zabluzhdenie. Esli dva ob容kta stalkivayutsya v vakuume, to nikakogo shuma voobshche ne vozniknet. Oshibka voznikaet ottogo, chto shum pripisyvayut stolknoveniyu, no oni teryayut iz vnimaniya rol' sredy, kotoraya perenosit energiyu ot ob容ktov k uhu.
Vse eto tol'ko podgotovka k obsuzhdeniyu razlichnyh urovnej smysla, kotorymi napolnen Kontrakrostihpunk. Dialog imeet i yavnoe i skrytoe soderzhanie. Naibolee yavnyj uroven' smysla v tom, chto zdes' prosto rasskazana nekotoraya istoriya. |tot "yavnyj" smysl chrezvychajno neyaven v tom znachenii, chto myslitel'nye processy, vovlechennye v ponimanie sobytij istorii (zapechatlennyh tol'ko v vide spleteniya chernyh chertochek na bumage) neveroyatno slozhny. Odnako my rassmotrim proishodyashchee v Dialoge v samom yavnom znachenii i predpolagaem, chto vsyakij chitayushchij na chelovecheskom yazyke ispol'zuet bolee-menee pohozhij "izomorfizm" i v rezul'tate izvlechet bolee-menee pohozhij smysl iz simvolov na bumagu.
GEB
Duglas R. Hofshtadter.
[ predydushchaya ]
[ oglavlenie ]
Perevod Aleksandra Semenova
Neprotivorechivost', Polnota i Geometriya
Vyshe ya ispol'zoval termin "izomorfizm" v kavychkah, ukazyvaya etim, chto ono dolzhno prinimat'sya s nekotoroj natyazhkoj. Utonchennyj process, kotoryj lezhit v osnove processa vospriyatiya i ponimaniya chelovecheskogo yazyka gorazdo slozhnej, chem operacii nad simvolami v tipichnyh formal'nyh sistemah. My dolzhny budem prinyat' (esli my hotim i dalee dumat' o smysle kak o proyavlenii izomorfizma) gorazdo bolee gibkuyu ideyu. Pridetsya priznat', chto izomorfizmy mogut byt' bolee shiroko privlecheny dlya ob座asneniya processa ponimaniya, chem bylo prinyato. Po moemu mneniyu, fakticheski, klyuchevym elementom v otvete na vopros "CHto takoe soznanie?" budet proniknovenie v sushchnost' "izomorfizma", kotoryj lezhit v osnove togo, chto my nazyvaem smyslom.
No dazhe v takom sluchae ya hotel by byt' neskol'ko bolee chetkim otnositel'no yavnogo smysla dannoj istorii. Snachala ya budu govorit' po povodu proigryvatelej i plastinok k nemu. Zdes' glavnyj moment v tom, chto imeetsya dva urovnya osmysleniya roli zvukovyh dorozhek plastinki. Uroven' I - eto muzyka. No "Muzyka", eto posledovatel'nost' kolebanij chastic vozduha ili posledovatel'nost' emocional'nyh reakcij v mozge? I to, i to. No prezhde chem vozniknut emocional'nye reakcii, dolzhny prisutstvovat' kolebaniya vozduha. Dalee, kolebaniya vozduha generiruyutsya iz zvukovyh dorozhek proigryvatelem. Proigryvatel' - otnositel'no prostoe ustrojstvo. Fakticheski, vy mozhete poluchit' zvuk napryamuyu, tol'ko provedya bulavkoj vdol' dorozhek zvukozapisi. Posle etoj stadii uho preobrazovyvaet zvukovye kolebaniya v impul'sy sluhovyh nejronov mozga. Dalee proishodit mnozhestvo etapov preobrazovanij v kore mozga, kotorye postepenno prevrashchayut zvukovye kolebaniya v slozhnoe spletenie emocional'nyh reakcij. |tot process slishkom slozhen dlya nas, chtoby, nachav v nem razbirat'sya zdes', k koncu knigi skol'ko-nibud' preuspet'. Poetomu, pozvol'te mne udovletvorit'sya rassuzhdeniyami ob "Pervom Urovne" soderzhaniya zvukovyh dorozhek kak o zvuke v vozduhe. Kakov zhe smysl Urovnya Dva dlya teh zhe dorozhek? |to rezonansnye kolebaniya, vozbuzhdennye v proigryvatele. |to soderzhanie mozhet proyavit' sebya tol'ko posle proyavleniya Urovnya Odin, kotoryj sam voznikaet neposredstvenno iz dorozhek, tak kak kolebaniya proigryvatelya vyzyvayutsya tol'ko kolebaniyami vozduha. Poluchaetsya chto Vtoroj Uroven' smysla zavisit ot cepi dvuh izomorfizmov:
(1) Izomorfizm mezhdu uglubleniem proizvol'noj formy na poverhnosti plastinki i vibraciej vozduha.
(2) Izomorfizm mezhdu vibraciej vozduha i kolebaniyami proigryvatelya.
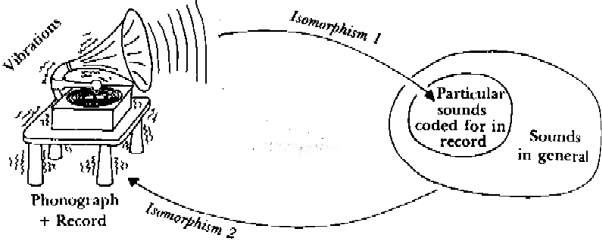
RIS. 20. Shematicheskoe predstavlenie principa, lezhashchego v osnove Teoremy Gedelya: dva otobrazheniya "odin v drugoj", kotorye imeyut neozhidannyj effekt bumeranga. Pervoe otobrazhaet formu dorozhek zvukozapisi na zvuki, proizvodimye fonografom. I tut zhe (znakomoe, no obychno ignoriruemoe yavlenie) zvuki vyzyvayut kolebaniya fonografa. Obratite vnimanie, chto vtoroe otobrazhenie sushchestvuet nezavisimo ot pervogo. Zvuk iz lyubogo istochnika (ne tol'ko proizvedennogo fonografom neposredstvenno) prichinit podobnye kolebaniya. Perefraziruya Teoremu Gedelya skazhem, chto dlya lyubogo proigryvatelya, imeyutsya zapisi, kotorye na nem nel'zya sygrat', potomu, chto oni privodyat ego k kosvennomu samorazrushenie. [Risunok avtora]
|ta cep' izomorfizmov pokazana na ris. 20. Zamet'te, chto izomorfizm 1 - tot, kotoryj sootvetstvuet Pervomu Urovnyu soderzhaniya dorozhek. Vtoroj Uroven' soderzhaniya gramzapisi yavlyaetsya menee yavnym, chem Pervyj, potomu chto on proyavlyaetsya tol'ko v cepi dvuh izomorfizmov. |tot vtoroj uroven' soderzhaniya, kotoryj i vyzyvaet "nepriyatnye posledstviya" - gibel' proigryvatelya. CHto interesno, izvlekaya Pervyj Uroven', my odnovremenno izvlekaem Vtoroj. I net nikakogo sposoba izvlech' Pervyj bez Vtorogo. Tak chto, Vtoroj byl iznachal'no neyavnym soderzhanie gramzapisi, kotoroe obernulos' protiv nee zhe, razrushiv plastinku.
Podobnyj kommentarij primenim i k kubku. Odno otlichie - perehod ot bukv alfavita k notnym znakam- eto eshche odni uroven' izomorfizma, kotoryj my mozhem nazvat' "transkripciya". Vybrannyj termin sleduet iz ego perevoda - preobrazovanie muzykal'nyh not v muzykal'nyj zvuk. Dalee zvuk, to est' kolebaniya vozduha, vozdejstvuet obratno na kubok tochno takzhe, kak on vozdejstvuet na lyuboj obrazec iz predlozhennyh proigryvatelej.
Skrytyj smysl Kontrakrostihpunkta
CHto po povodu skrytyh smyslov Dialoga? (Ih dejstvitel'no neskol'ko). Samyj prostoj iz nih, byl uzhe upomyanut. A imenno to, chto sobytiya v dvuh chastyah Dialoga priblizitel'no izomorfny drug k drugu. Fonograf stanovit'sya skripkoj, CHerepaha stanovit'sya Ahillesom, Krab stanovit'sya CHerepahoj. Dorozhki zvukozapisi stanovyatsya avtografom, gravirovannym na kubke i t.d. Kak tol'ko vy obnaruzhivaete etot prostoj izomorfizm, vy mozhete prodvinut'sya dal'she. Sledite: v pervoj polovine CHerepaha istochnik vseh zol, v to vremya kak vo vtoroj polovine on - zhertva. Kak vy znaete, ego sobstvennyj metod, obrashchaetsya protiv nego zhe nepriyatnymi posledstviyami! Napominaet li eto o nepriyatnostyah voznikshih iz muzyki ego plastinok, ili nadpisi na kubke? Ili eto napominaet o prekrasnoj kollekcii bumerangov, sobrannyh CHerepahoj?
Poetomu vy dazhe mozhete videt' izomorfizm mezhdu dvumya urovnyami istorii. My priravnivaem sposob, kakim gramzapisi i kubki bumerangom b'yut sami po sebe so sposobom, kakimi zhestkie metody CHerepahi bumerangom b'yut po nemu samomu. Obratite na eto vnimanie.
Vzaimnoe otobrazhenie mezhdu Kontrakrostihpunktom i Teoremoj Gedelya
Vozmozhno, vas eto uzhe slegka ukachalo - no luchshee vperedi. (Po suti, nekotorye urovni skrytogo smysla my zdes' dazhe ne budem obsuzhdat', oni ostavleny dlya vas, kak zagadka) Samoj glubokoj prichinoj dlya napisaniya etogo Dialoga bylo stremlenie illyustrirovat' Teoremu Gedelya, kotoraya, kak ya skazal v predislovii, opiraetsya na dva razlichnyh urovnya smysla utverzhdenij teorii chisel. Kazhdaya iz polovinok kontrakrostihpunkta - "izomorfnaya kopiya" Teoremy Gedelya. Poskol'ku eto otobrazhenie - central'naya ideya Dialoga i ona dovol'no slozhnoe, ya tshchatel'no prorisuyu ego nizhe:
Da, dejstvitel'no, istoriya s nepriyatnymi posledstviyami proishodit na dvuh urovnyah...
Uroven' Odin. Kubok i gramzapisi, kotorye privodyat k nepriyatnym posledstviyam.
Uroven' Dva. D'yavol'skij metod CHerepahi (ispol'zovat' skrytoe soderzhanie, chtoby vyzyvat' nepriyatnye posledstviya) vyzyvaet nepriyatnye posledstviya.
Proigryvatel' nizkogo kachestva <==> "slabaya" aksiomaticheskaya sistema
Vysokokachestvennyj proigryvatel' <==> "sil'naya" aksiomaticheskaya sistema
"Sovershennyj" proigryvatel' <==> polnaya aksiomatika teorii chisel
"Proekt" fonografa <==> aksiomy i pravila formal'noj sistemy
Gramzapisi <==> cepochki formal'noj sistemy
Proigryvaemye zapisi <==> teorema aksiomaticheskoj sistemy
Ne proigryvaemye zapisi <==> ne teoremy aksiomaticheskoj sistemy
Zvuk <==> istinnye utverzhdeniya teorii chisel
Vosproizvodimyj zvuk <==> interpretiruemaya teorema sistemy
Ne vosproizvodimyj zvuk <==> istinnoe utverzhdenie, ne yavlyayushcheesya teoremoj
Nazvanie pesni: <==> skrytyj smysl vyrazheniya Gedelya:
"YA Ne mogu Byt' Sygran "YA ne mogu Byt' Poluchen
Na proigryvatele X " v Formal'noj Sisteme X "
|to ne polnoe opisanie izomorfizma mezhdu Teoremoj Gedelya i Kontrakrostihpunktom, no eto - yadro, samoe glavnoe. Ne stoit volnovat'sya po povodu togo, polnost'yu li vy uhvatili smysl Teoremy Gedelya k nastoyashchemu momentu. Vperedi vse eshche imeetsya neskol'ko glav, kotorye sleduet preodolet', prezhde chem my dostignem celi. Odnako, chitaya etot Dialog, vy ulovili duh teoremy Gedelya bez neobhodimosti doskonal'nogo znaniya ee. Teper' ya ostavlyu vas s etim, chto by razyskat' drugie skrytye smysly v Kontrakrostihpunkte. "Quaerendo invenietis!"
Iskusstvo fugi
Neskol'ko slov ob Iskusstve fugi... Sozdannoe v poslednij god zhizni Baha, ono predstavlyaet soboj osnovannoe na odnoj teme sobranie vosemnadcati fug. Ochevidno, napisanie Muzykal'nogo Prinosheniya sluzhilo istochnikom vdohnoveniya Bahu. On reshil napisat' novoe sobranie fug, kotorye byli by osnovany na odnoj ochen' prostoj teme. Var'iruya ee, on hotel prodemonstrirovat' shirokie vozmozhnosti, prisushchie forme. V Iskusstve fugi Bah ispol'zuet odnu edinstvennuyu temu, no samymi raznymi virtuoznymi sposobami. Vsya raboty vypolnena v edinom klyuche. Bol'shinstvo fug imeyut chetyre golosa, i oni postepenno uvelichivayutsya v slozhnosti i glubine vyrazheniya. V konce oni podnimayutsya k takim utonchennym vysotam, chto, kazhetsya, net nikakoj bol'she vozmozhnosti razvivat' slozhnost' muzyki dal'she. I vse zhe on eto delaet . . . do poslednego.
Kontrapunkt
Obstoyatel'stva, kotorye prervali napisanie Iskusstva fugi (zdes' nado vspomnit' obstoyatel'stva zhizni Baha) zaklyuchalos' v ego zrenii, bespokoivshem ego na protyazhenii mnogih let. Bah hotel sdelat' operaciyu. |to bylo sdelano, odnako rezul'taty okazalis' ochen' plohimi, i kak posledstviya on poteryal zrenie voobshche na poslednej chasti goda svoej zhizni. Odnako eto ne ostanovilo ego energichnoj raboty nad monumental'nym tvoreniem. Ego cel' - predstavit' polnyj spektr vozmozhnyh variantov fug i mnogokratnoe ispol'zovanie dlya etogo odnoj temy bylo vazhnym faktorom. V tom, chto on planiroval kak predposlednyaya fuga, on vstavil svoe sobstvennoe imya, zakodirovannoe v notah kak tret'ya tema. Odnako k etomu momentu vremeni ego sostoyanie zdorov'ya stalo nastol'ko somnitel'nym, chto on vynuzhden byl otkazat'sya ot raboty nad vzleleyannym proektom. V nachale bolezni on sumel prodiktovat' zyatyu zaklyuchitel'nuyu chast' horala, o kotoroj biograf Baha Fokel' (Forkel) napisal: "Vyrazhenie pokornogo smireniya i nabozhnosti vsegda ohvatyvayut menya, kogda ya igral eto. Tak chto ya eda smogu skazat', chto by predpochel poteryat' - etot Hor, ili konec poslednej fugi."
Problemy, vyzvannye rezul'tatami Gedelya
CHerepaha utverzhdaet, chto nedostatochno moshchnyj proigryvatel' mozhet byt' sovershenen v tom smysle, chto on mozhet vosproizvodit' kazhdyj vozmozhnyj zvuk gramzapisi. Gedel' govorit, chto nedostatochno moshchnaya formal'naya sistema mozhet byt' sovershenna, v smysle vosproizvedeniya kazhdogo otdel'nogo istinnogo utverzhdeniya kak teoremy. No tak zhe kak CHerepaha utverzhdaet o proigryvatele, etot fakt tol'ko pohozh na defekt, esli vy imeete nerealistichnye ozhidaniya otnositel'no togo, chto formal'naya sistema dolzhna delat'. Odnako matematiki vstupili v eto stoletie (XX -A. S.) imenno s takimi nerealistichnymi ozhidaniyami. Polagaya, chto aksiomaticheskie rassuzhdeniya okazhutsya panaceej ot vseh bed. Oni vyyasnili obratnoe, tol'ko v 1931 godu. Fakt, chto istina ne vmeshchaetsya v "prostranstv" teorem lyuboj dannoj formal'noj sisteme, nazyvaetsya "nepolnotoj" sistemy.
Izmenennaya pq-sistema i protivorechivost'
CHtoby uvidet' situaciyu bolee realistichno, nuzhno gorazdo glubzhe videt', pochemu i kak smysl v aksiomaticheskih sistemah obrazuetsya izomorfnymi svyazyami. I ya polagayu, chto eto vedet eshche k bolee romanticheskomu vzglyadu na situaciyu. Poetomu teper' my prodolzhim rassmatrivat' nekotorye drugie aspekty otnoshenij mezhdu smyslom i formoj. I nash pervyj shag - my dolzhny sdelat' novuyu formal'nuyu sistemu, slegka izmeniv starogo druga, pq-sistemu. My dobavim eshche odnu shemu aksiom (sohraniv pervonachal'nuyu shemu, tak zhe kak i edinstvennoe pravilo vyvoda):
YAsno, chto togda _ _ p _ q _ _ - yavlyaetsya teoremoj v novoj sisteme (vse aksiomy -teoremy) i tak zhe _ _p _ _ q _ _ _. I vse zhe ih interpretaciya sootvetstvenno, "2 plyus 1 ravno 2", i "2 plyus 2 ravno 3". No legko zametit', chto nasha novaya sistema budet soderzhat' mnogo lozhnyh utverzhdenij (esli vy budete rassmatrivat' cepochki kak utverzhdeniya). Takim obrazom, nasha novaya sistema neposledovatel'na ili protivorechiva s vneshnim mirom.
Neprotivorechivost' vosstanovlena
Davajte, naprimer, predpolozhim, chto my po-drugomu interpretiruem simvol q, ostaviv vse ostal'nye interpretacii - temi zhe. V chastnosti, interpretiruem q frazoj "bol'she ili ravno". Teper' nashi "protivorechashchie" teoremy _ p _ q _ i _ p _ q _ _ poluchat'sya vpolne sovmestimymi: "1 plyus 1 bol'she ili ravno 1" i "1 plyus 1 bol'she ili ravno 2". My odnovremenno izbavilis' (1) ot protivorechiya s vneshnim mirom i (2) ot vnutrennih protivorechij. Nasha novaya interpretaciya - osmyslennaya interpretaciya, v to vremya kak pervonachal'naya, nesomnenno, bessmyslenna. To est' ona bessmyslenna v nashej novoj sisteme, a dlya pervonachal'noj pq-sistemy ona podhodit po-prezhnemu prekrasno. No pervonachal'naya interpretaciya kazhetsya bessmyslennoj i nelepoj, esli primenit' ee k novoj, pq-sistem. Ona zdes' nastol'ko zhe umestna, kak "yablochno-loshadino-schastlivuaya" interpretaciya umestna k staroj pq-sisteme.
Istoriya Evklidovoj geometrii
Hotya ya i pytalsya zastat' vas vrasploh i nemnogo udivit', no etot urok o interpretacii simvolov slovami, ne kazhetsya slishkom trudnym kak tol'ko vy vidite sut' predmeta. No na praktike eto ne vsegda tak. V etom sostoyal odin iz samyh glubokih urokov matematiki devyatnadcatogo stoletiya!
Vse nachalos' s Evklida, kotoryj okolo 300 goda do nashej ery sistematiziroval i interpretiroval vse, chto bylo izvestno otnositel'no planimetrii i stereometrii v ego dni.
RIS 21. Vavilonskaya bashnya, M. C. Escher (gravyura na dereve, 1928).
CHem obydennee, chem chashche upotreblyaetsya slovo, tem bol'she associacij my imeem s etim slovom i tem glubzhe skryty korni ego soderzhaniya.
Hotya on nikogda etogo yavno i ne govoril, no Evklid rassmatrival etot postulat kak nizhe utverzhdenie rangom po otnosheniyu k drugim, potomu chto on ne ispol'zoval ego v dokazatel'stvah pervyh dvadcati vos'mi utverzhdenij. Takim obrazom, pervye dvadcat' vosem' utverzhdenij prinadlezhat tomu, chto moglo by nazyvat'sya "geometriya s chetyr'mya postulatami" - ta chast' geometrii, kotoraya mozhet byt' poluchena na osnovanii pervyh chetyreh postulatov Nachal bez pomoshchi pyatogo (ee takzhe, chasto nazyvayut "absolyutnoj geometriej"). Konechno, Evklid skoree predpochel by vyvesti etogo "gadkogo utenka" iz ostal'nyh postulatov, chem prinimat' ego. No on ne nashel dlya nego nikakogo dokazatel'stva i vynuzhden byl prinyat' kak postulat.
Mnogolikij Neevklid
Giloramo Sakcheri (Girolamo Saccheri 1667-1733) zhil priblizitel'no v to zhe vremya chto i Bah. On imel ambicii osvobodit' geometriyu Evklida ot nedostatkov. Osnovyvayas' na nekotoryh bolee rannih rabotah, sdelannyh im v logike, on reshil poprobovat' novyj podhod k dokazatel'stvu znamenitogo pyatogo postulata. Predpolozhim, chto vy prinimaete protivopolozhnoe emu utverzhdenie, i rabotaete s nim kak s pyatym postulatom. . . Estestvenno, chto cherez nekotoroe vremya vy pridete k protivorechiyu. Tak kak nikakaya matematicheskaya sistema ne mozhet soderzhat' protivorechie, vy tem samym dokazhete neobosnovannost' predlozhennogo vami postulata i kak sledstvie - obosnovannost' pyatogo postulat Evklida. My ne stanem zdes' rassmatrivat' podrobnosti. Udovletvorimsya tem, chto soobshchim: s bol'shim masterstvom Sakcheri vystroil utverzhdenie za utverzhdeniem v ramkah "geometrii Sakcheri" i v konce koncov eto ego utomilo. V kakoj-to moment emu pokazalos', chto on poluchil utverzhdenie, kotoroe "protivorechilo prirode pryamyh linij". Imenno eto, kak on nadeyalsya, i est' davno razyskivaemoe protivorechie. Zdes' on prinyal reshenie izdat' svoyu rabotu pod nazvaniem "Evklid, svobodnyj ot vseh slabyh mest" i na etom issyak.
Ty ne dolzhen i pytat'sya podhodit' k voprosu o parallel'nyh. YA proshel etot put' do konca. YA peresek etu bezgranichnuyu noch', kotoraya pogasila ves' svet i vsyu radost' moej zhizni. YA umolyayu tebya ostavit' vopros o parallelyah v pokoe. . . ya dumal, chto smogu pozhertvovat' soboj radi istiny. YA byl gotov stat' muchenikom, kotoryj ispravit porok geometrii i vernet ee ochishchennoj chelovechestvu. YA vypolnil chudovishchnuyu, ogromnuyu rabotu. Moi rezul'taty gorazdo luchshe, chem u drugih. I vse zhe ya ne dostig polnogo udovletvoreniya. Istina v tom, chto si paullum a summo discessit, vergit ad imum. YA povernul obratno, kogda uvidal, chto nikto ne mozhet dostignut' toj storony etoj nochi. YA povernul obratno bezuteshnyj, polnyj zhalosti k vsemu chelovechestvu. . . ya puteshestvoval minuya vse rify etogo adskogo Mertvogo Morya, no vsegda vozvrashchalsya so slomannoj machtoj i porvannym parusom. Ruiny moih pozicij i moya starost' - vse, chto ya imeyu v itoge. YA neosmotritel'no risknul svoej zhizn'yu i Caesar aut nihil.
No pozzhe, kogda ego ne pereubezhdennyj syn dejstvitel'no imel "koe chto", on ubezhdal ego izdat' rezul'taty ne meshkaya, napominaya ob odnovremennom poyavleniya pravil'nyh rezul'tatov, stol' chasto sluchayushchihsya v mire nauchnyh otkrytij:
Kogda nastupaet vremya dlya nekotoryh veshchej, oni poyavlyayutsya v samyh raznyh mestah na maner fialok, probivayushchihsya povsyudu rannej vesnoj.
Naskol'ko zhe eto bylo spravedlivo v sluchae neevklidovoj geometrii! V Germanii neposredstvenno Gauss i nekotorye drugie issledovateli bolee-menee nezavisimo drug ot druga natolknulis' na neevklidovy idei. V chastnosti, advokata SHvejkarta (F. K. Schweikart) v 1818 godu poslal Gaussu stranicu opisyvayushchuyu novuyu "astral'nuyu" geometriyu. Plemyannik SHvejkerta, Taurinus (F. A. Taurinus) sozdal neevklidovu trigonometriyu, a student Gaussa, Vashter (F. L. Wachter), kotoryj umer v 1817 godu, v vozraste 25-ti let, nashel nekotorye glubokih rezul'tata v neevklidovoj geometrii.
Neopredelennye terminy
|to dlya nas znakomo. V chastnosti, eto vozvrashchaet nas k pq-sisteme i ee variantu, v kotorom simvoly priobretayut passivnoe znachenie v zavisimosti ot ih rolej v teoremah. Simvol q osobenno interesen, posle togo, kak ego "znachenie" bylo zameneno s dobavleniem novoj shemy aksiom. Analogichnym sposobom mozhno pozvolit' i smyslu terminov "tochka", "pryamaya" i tak dalee, opredelyat'sya naborom teorem (ili suzhdenij) v kotoryh oni vstrechayutsya. |tot sposob byl velikolepno realizovan issledovatelyami neevklidovoj geometrii. Oni nashli razlichnye vidy neevklidovyh konfiguracij, otvergaya pyatyj postulat Evklida razlichnymi sposobami i rassmatrivaya posledstviya takogo shaga. Strogo govorya, oni (i Sakcheri tozhe) ne otricali pyatyj postulat neposredstvenno. Oni otricali ekvivalentnyj postulat, kotoryj zvuchit sleduyushchim obrazom:
Vtoraya pryamaya liniya, kak schitaetsya, parallel'na pervoj. Esli vy utverzhdaete, chto nikakoj takoj linii ne sushchestvuet, to vy poluchite ellipticheskuyu geometriyu, esli vy utverzhdaete chto, po krajnej mere, dve takih linii sushchestvuyut, to vy poluchite giperbolicheskuyu geometriyu. Kstati, prichina chto takie raznovidnosti vse eshche nazyvayutsya "konfiguraciyami" v tom, chto osnovnoj element ostaetsya neizmennym - chetyre pervyh postulata geometrii ostayutsya osnovnoj chast'yu lyuboj iz geometrij. Prisutstvie minimal'nogo yadra delaet dlya razuma vospriyatie ih svojstv kak svojstv hot' i nekotorogo osobogo vida, no vse zhe geometricheskogo prostranstva, dazhe esli eto prostranstvo ne stol' intuitivno ponyatno kak obychnoe prostranstvo.
Vozmozhnost' razlichnoj interpretacii
Polnaya formalizaciya geometrii sovershila by reshitel'nyj shag esli by sdelat' kazhdyj termin neopredelennym, to est' prevratit' kazhdyj termin v "bessmyslennyj" simvol formal'noj sistemy. YA vzyal v kavychki "bessmyslennyj" potomu chto, kak vy znaete, simvoly avtomaticheski priobretayut passivnyj smysl v sootvetstvii s teoremami, v kotoryh oni vstrechayutsya. |to konechno, drugoj vopros, obnaruzhivayut li lyudi etot smysl, kak eto trebuetsya, vo vsem mnozhestve idej, kotoryj mozhet byt' svyazan izomorfizmom v simvolah formal'noj sistemy. Esli nachinat' s idei formalizacii geometrii, to, po-vidimomu, v nej imeetsya takaya opredelennaya interpretaciya kazhdogo simvola, chto ih passivnoe znachenie bylo vklyucheno v sistemu. Imenno eto ya delal dlya p i q, kogda nachal sozdavat' pq-sistemu.
Raznovidnosti neprotivorechivostej
My govorili otnositel'no "posledovatel'nosti" i "neposledovatel'nosti", bez togo, chtoby opredelit', chto eto takoe. My polozhilis' na dobrye, starye, obydennye ponyatiya. No teper' opredelim tochno, chto predpolagaetsya pod posledovatel'nost'yu ili neprotivorechivost'yu formal'noj sistemy (vmeste s interpretaciej): eto esli kazhdaya teorema, kogda ona interpretiruetsya, stanovit'sya istinnym utverzhdeniem. I my budem govorit', chto protivorechivost' voznikaet togda, kogda, po krajnej mere, est' hotya by odno lozhnoe utverzhdenie sredi interpretiruemyh teorem.
V odin den', vnezapno k Bahu vernulos' zrenie. No neskol'kimi chasami pozzhe on perenes udar i spustya desyat' dnej umer, ostaviv drugim razmyshlyat' o nepolnote Iskusstva fugi. Interesno, mozhno li poetomu skazat', chto zdes' Bah dostig samossylki?
Naibolee ozadachivayushchij fakt, otnositel'no metodov dokazatel'stva Gedelya, to, chto on ispol'zuet metody rassuzhdenij, kotorye, po vsej vidimosti, ne mogut byt' "inkapsulirovany" - oni soprotivlyayutsya vklyucheniyu v lyubuyu formal'nuyu sistemu. Takim obrazom, na pervyj vzglyad, kazhetsya, chto Gedel' raskopal do nastoyashchego vremeni neizvestnoe, no gluboko sushchestvennoe razlichie mezhdu chelovecheskimi rassuzhdeniyami i rassuzhdeniyami mehanicheskimi. |to misticheskoe razlichie v moshchnosti mezhdu zhivymi i nezhivymi sistemami otobrazhaetsya v nesootvetstvii mezhdu ponyatiem istiny i prostranstva teorem. . . ili, po krajnej mere, yavlyaetsya "romanticheskim" sposobom smotret' na situaciyu.
Shema aksiom II: Esli h - cepochka defisov to xp_qx aksioma.
Kak budto etogo bylo malo, no my tak zhe imeem vnutrennie problemy s nashej novoj sistemoj, tak kak ona soderzhit utverzhdeniya, kotorye ne soglasuyutsya drug s drugom, tipa
_ p _ q _ _ (staraya aksioma) i _ r _ q _ (novaya aksioma). Tak chto nasha sistema protivorechiva vo vtorom smysle - vnutrenne.
Bylo by, poetomu, edinstvenno razumnym resheniem - vybrosit' etu sistemu? Vryad li. YA special'no predstavil eti "protivorechiya", chtoby povodit' vas za nos. YA proboval vyrazit' nechetko-predstavimye argumenty nastol'ko argumentirovano, naskol'ko eto vozmozhno, chtoby vvesti vas v zabluzhdenie. Vozmozhno, vy legko ulovili podvoh v tom, chto ya tut izlozhil. Kriticheskaya oshibka proizoshla togda, kogda ya bez somnenij prinyal te zhe samye interpretiruyushchie slova dlya novoj sistemy, chto i dlya staroj. Pomnite, imelsya tol'ko odin povod dlya togo, chtoby ispol'zovat' dlya interpretacii te slov, v proshloj glave, i prichina byla v tom, chto simvoly dejstvovali izomorfno k ideyam, oni byli soglasovany s interpretaciej. No kogda vy izmenyaete pravila, kotorye upravlyayut sistemoj, vy neizbezhno razrushite izomorfizm. I etomu nichem nel'zya pomoch'. Poetomu vse problemy, kotorye pritvorno oplakivalis' v predydushchih abzacah, okazalis' poddel'nymi. Oni mogut obratit'sya v nichto, esli vy sootvetstvenno dadite inoe tolkovanie nekotorym simvolam sistemy. Zamet'te, ya skazal "nekotorym". Ne obyazatel'no chtoby vse simvoly otobrazhalis' imenno na novye ponyatiya. Nekotorye mogut sohranyat' svoi starye "znacheniya", v to vremya kak drugie izmenyat'sya.
Okonchatel'nyj trud, Nachal Evklida, byli nastol'ko stroen i prochen, chto stali fakticheski bibliej geometrii v techenii bolee chem dvuh tysyach let. Nachala - naibolee nepokolebimyj trud vseh vremen. Pochemu?
Osnovnaya prichina v tom, chto Evklid byl zakonodatelem strogosti v matematike. Nachala nachinayutsya s ochen' prostyh idej, opredelenij i t.d. Vse eto postepenno vyrastaet v obshirnoe zdanie rezul'tatov, organizovannyh takim sposobom, chto lyuboj konkretnyj rezul'tat zavisel tol'ko ot predshestvuyushchih rezul'tatov. Takim obrazom, imelsya opredelennyj plan raboty, struktura kotorogo sdelala vsyu gromadu geometrii strojnym i prochnym sooruzheniem.
 Odnako arhitektura etoj konstrukcii byla otlichnoj ot, naprimer, privychnoj nam arhitektury neboskreba (sm. ris.21) V poslednem sluchae, esli zdanie stoit, to eto dokazyvaet, chto vse ego strukturnye elementy derzhat ego nagruzku. No v knige po geometrii, kogda kazhdoe suzhdenie trebuet, chtoby ono logicheski sledovalo iz bolee rannih suzhdenij, ne budet nikakogo krusheniya, esli odno iz dokazatel'stv nedejstvitel'no. Zdes' balki i rasporki ne fizicheskie, a abstraktnye ob容kty. Fakticheski, v Nachalah Evklida materialom dlya postroeniya dokazatel'stv sluzhil chelovecheskij yazyk. YAzyk- neulovimaya, zybkaya sreda hitrospletennyh otnoshenij i smyslov s ogromnym mnozhestvom nevidimyh lovushek. CHto zhe togda sluzhit konstrukcionnoj oporoj v Nachalah? Mozhno li utverzhdat', chto vse zdanie vyvodov podderzhivaetsya zhestkimi strukturnymi elementami ili v nem imeyutsya konstrukcionnye slabosti i proschety?
Odnako arhitektura etoj konstrukcii byla otlichnoj ot, naprimer, privychnoj nam arhitektury neboskreba (sm. ris.21) V poslednem sluchae, esli zdanie stoit, to eto dokazyvaet, chto vse ego strukturnye elementy derzhat ego nagruzku. No v knige po geometrii, kogda kazhdoe suzhdenie trebuet, chtoby ono logicheski sledovalo iz bolee rannih suzhdenij, ne budet nikakogo krusheniya, esli odno iz dokazatel'stv nedejstvitel'no. Zdes' balki i rasporki ne fizicheskie, a abstraktnye ob容kty. Fakticheski, v Nachalah Evklida materialom dlya postroeniya dokazatel'stv sluzhil chelovecheskij yazyk. YAzyk- neulovimaya, zybkaya sreda hitrospletennyh otnoshenij i smyslov s ogromnym mnozhestvom nevidimyh lovushek. CHto zhe togda sluzhit konstrukcionnoj oporoj v Nachalah? Mozhno li utverzhdat', chto vse zdanie vyvodov podderzhivaetsya zhestkimi strukturnymi elementami ili v nem imeyutsya konstrukcionnye slabosti i proschety?
Kazhdoe slovo, kotoroe my ispol'zuem, nadeleno dlya nas smyslom, kotoryj i rukovodit nami, kogda my ego primenyaem.
Poetomu kogda kto-to daet opredelenie dlya shiroko upotreblyaemogo slova v nadezhde, chto my ostanemsya v ego ramkah, to eto neizbezhno privedet k tomu, chto my ne budem pol'zovat'sya predlozhennym opredeleniem, no budem vmesto etogo rukovodstvovat'sya (v znachitel'noj stepeni podsoznatel'no) tem, chto nash um vyhvatit iz podvalov svoih associacij. YA upominayu ob etom potomu chto eto raznovidnost' problemy, kotoruyu Evklid sozdal v svoih Nachalah, delaya popytku dat' opredelenie obychnyh, shiroko upotreblyaemyh slov tipa "tochka", "pryamaya liniya", "okruzhnost'" i t.d. Kak vy mozhete opredelit' chto-to takoe, o chem kazhdyj uzhe imeet yasnoe predstavlenie? Edinstvennyj sposob - ukazat', chto vashi slova, kak predpolagaetsya, yavlyayutsya tehnicheskimi terminami i ih nel'zya putat' s kazhdodnevnym znacheniem etih slov, kotorye tol'ko pohozhi na nih po zvuchaniyu. Horosho. Evklid ne delal etogo, potomu chto on chuvstvoval, chto tochki i linii ego Nachala byli v dejstvitel'nosti tochkami i liniyami real'nogo mira. Poetomu ne buduchi uverennym chto vse postoronnie associacii byli rasseyany Evklid priglashal chitatelej pozvolit' svoim associaciyam voznikat' svobodno. . .
|to vyglyadit pochti anarhiej i ne sovsem spravedlivo po otnosheniyu k Evklidu. On zapisyval aksiomy ili postulaty, kotorye, kak predpolagal, ispol'zovalis' v dokazatel'stvah utverzhdenij. Fakticheski, nichego drugogo krome teh aksiom i postulatov, kak on nadeyalsya, ne ispol'zovalos'. No v etom on oshibalsya. Neizbezhnym posledstviem ispol'zovaniya im obychnyh slov bylo to, chto nekotorye iz obrazov vyzvannyh temi slovami prokralis' v dokazatel'stva, kotorye on sozdaval. Odnako esli vy chitaete dokazatel'stva v Nachalah, to ne uvidite yavnyh "skachkov" v rassuzhdeniyah. Naprotiv oni ochen' tonkie. Evklid byl pronicatel'nyj myslitel' i ne sdelal nikakih yavnyh oshibok. Tem ne menee, dyry tam imeyutsya, tem samym, vyzyvaya nekotoryj deficit strogosti v etoj klassicheskoj rabote. No na eto ne stoit zhalovat'sya. Nuzhno prosto razlichat' absolyutnuyu strogost' i otnositel'nuyu strogost' rassuzhdenij. V konce koncov, nedostatok u Evklida absolyutnoj strogosti posluzhil prichinoj nekotoryh iz naibolee plodotvornyh novovvedenij v matematike spustya bolee chem dve tysyachi let posle togo kak on napisal etu rabotu.
Evklid ustanovil pyat' postulatov, kotorye nuzhno ispol'zovat' kak "absolyutnoe osnovanie" beskonechnogo neboskreba geometrii, v kotorom ego Nachala sostavlyayut tol'ko pervye neskol'ko sot etazhej. Pervye chetyre postulata dovol'no kratkie i izyashchnye.
(1) Otrezok pryamoj linii mozhet byt' procherchen, esli soedinit' dve tochki.
Pyatyj postulat, odnako, ne razdelyaet izyashchestva brat'ev:
(2) Lyuboj otrezok pryamoj linii mozhet byt' neopredelenno dolgo prodleno vdol' nee.
(3) Dan nekotoryj otrezok pryamoj linii. Okruzhnost' mozhet byt' postroena, esli imet' otrezok kak radius i odnu tochku na konce otrezka ispol'zovat' kak centr.
(4) Vse pryamye ugly kongruentny.
(5) Esli provedeny dve linii, kotorye peresekayutsya tret'ej liniej takim obrazom, chto summa vnutrennih uglov na dannoj storone men'she chem dva pryamyh ugla, togda eti dve pryamyh linii neizbezhno dolzhny peresech'sya drug s drugom na etoj storone, esli ih prodolzhit' neopredelenno dolgo
.
No posledovateli Evklida ne ispytyvali nikakogo schast'ya ot neobhodimosti prinimat' pyatyj postulat. na protyazhenii stoletij, neveroyatnoe chislo lyudej tratili neveroyatnoe chislo let svoej zhizni v popytke dokazat', chto pyatyj postulat byl sam po sebe rezul'tat pervyh chetyreh postulatov geometrii. V 1763 godu, po krajnej mere, dvadcat' vosem' razlichnyh dokazatel'stv etogo byli izdany. I vse -oshibochnye! Vse byli raskritikovany v dissertacii Kligela (G. S. Kliigel). |ti oshibochnye dokazatel'stva smeshivali kazhdodnevnuyu intuiciyu i strogo formal'nye svojstva.
Smelo mozhno skazat', chto segodnya edva li lyuboe iz etih "dokazatel'stv" sostavlyaet kakoj libo matematicheskij ili istoricheskij interes. No est' i isklyucheniya.
No sdelav tak, on lishil sebya bol'shoj posmertnoj slavy, tak kak on nevol'no obnaruzhil to, chto otkrylos' pozzhe, nazvannoe v posledstvii "giperbolicheskaya geometriya". Pyatnadcat'yu godami posle Sakcheri, Lambert (J. H. Lambert) tozhe "proshel mimo celi", na sej raz, projdya dazhe blizhe. Proshel mimo nastol'ko blizko, naskol'ko eto bylo vozmozhno. Nakonec sorokami godami pozzhe Lamberta i devyanosto godami posle Sakcheri neevklidova geometriya byla priznana tem chem ona est'. Ee odnovremenno, kak eto neob座asnimo byvaet, otkryl vengerskij matematik Johan Bol'yai (Johann Bolyai) v vozraste 21 god i russkij matematik Nikolaj Lobachevskij, kotoromu ispolnilos' tridcat'. Po ironii sud'by v etot zhe god velikij francuzskij matematik Andran-Mari Legandr (Adrien-Marie Legendre) pridumal to, chto, kak on byl uveren, bylo dokazatel'stvom pyatogo postulata Evklida, ochen' blizkoe k tomu, chto predlozhil Sakcheri.
Kstati otec Bol'yai, Vol'fgan Bol'yai (Wolfgang Bolyai), blizkij drug velikogo Gaussa, vlozhil mnogo sil v popytku dokazat' pyatyj postulat Evklida. V pis'me svoemu synu Johanu on proboval otgovorit' ego ot razmyshlenij nad etim voprosom:
Klyuch k neevklidovoj geometrii - "pryamye rassuzhdeniya" otnositel'no vyskazyvanij, kotorye poyavlyayutsya v konstrukciyah podobnyh geometriyam Sakcheri i Lamberta. Vyskazyvaniya Sakcheri "protivorechat svojstvam pryamyh linij" tol'ko esli vy ne mozhete osvobodit' sebya ot predvzyatogo ponimaniya togo, chto dolzhna oznachat' "pryamaya liniya". Esli zhe vy smozhete izbavit' sebya ot etih predvzyatyh obrazov i prosto pozvolite "pryamoj linii" byt' chem-to, chto udovletvoryaet novym suzhdeniyam, to vy dostigli radikal'no novoj tochki zreniya.
Dana lyubaya pryamaya i tochka raspolozhennaya ne na etoj pryamoj. Sushchestvuet odna i tol'ko odna pryamaya liniya, kotoraya prohodit cherez etu tochku i nikogda ne peresekaet pervuyu pryamuyu nezavisimo ot togo, kak daleko oni prostirayutsya.
Fakticheski, ellipticheskaya geometriya legko vizualiziruetsya. Vse "tochki", "pryamye" i tak dalee dolzhny byt' chastyami poverhnosti v forme "sfera". YA budu pisat' "TOCHKA" esli ya imeyu v vidu special'noe znachenie etogo termina, i pozvol'te pisat' "tochka", kogda predpochtitelen obydennyj smysl. Togda my mozhem skazat', chto TOCHKA sostoit iz pary diametral'no protivopolozhnyh tochek sfery. PRYAMAYA - bol'shaya okruzhnost' na sfere (okruzhnost', podobnaya ekvatoru, kotoraya imeet centr v centre sfery) V takoj interpretacii vyskazyvaniya ellipticheskoj geometrii soderzhat slova tipa "TOCHKA" i "PRYAMAYA" i govoryat o "prodvizhenii na" poverhnosti sfery tak zhe kak o prodvizhenii na ploskosti. Obratite vnimanie, chto dve PRYAMYE peresekayutsya v dvuh strogo diametral'no protivopolozhnyh tochkah na sfere, to est' strogo v odnoj edinstvennoj TOCHKE! I tak zhe kak dve PRYAMYE opredelyayut TOCHKU, tak i dve TOCHKI opredelyayut PRYAMUYU.
Rassmatrivaya slova tipa "TOCHKA" i "PRYAMAYA" tak, kak budto oni imeyut tol'ko tot smysl, kotoryj skryt v suzhdeniyah iz kotoryh eti terminy proishodyat, my predprinimaem shag k polnoj formalizacii geometrii. Pervyj shag. Ved' eta polu-formal'naya versiya vse eshche ispol'zuet mnogo slov na obychnom yazyke s ih obydennym znacheniem (slova tipa "na", "esli", "i", "soedinit'", "soderzhit"). Obydennyj smysl bylo izgnan iz slov tipa "TOCHKA" i "PRYAMAYA" i v otlichii ot ostal'nyh terminov,
sledovatel'no, oni nazyvayutsya neopredelennymi terminami. Neopredelennye terminy podobno simvolam p i q pq-sistemy stanovyatsya opredelennymi v nekotorom smysle neyavno, v sovokupnosti vseh teh suzhdenij, gde oni vstrechayutsya, bystree, chem v lyubom yavnom opredelenii.
Mozhno utverzhdat', chto polnoe opredelenie neopredelennyh terminov nahoditsya isklyuchitel'no v postulatah i s momenta, kak suzhdeniya sleduyut iz nih, smysl terminov neyavno prisutstvuyut uzhe tam. Takoe predstavlenie govorilo by chto postulaty - eto neyavnoe opredelenie vseh neopredelennyh terminov, opredelyaemoe drugimi neopredelennymi terminami.
No mozhet imet'sya drugoj passivnyj smysl, kotoryj yavlyaetsya vpolne zametnym, odnako kotoryj vse zhe nikto ne zametil. Naprimer, imeyutsya udivitel'nye interpretacii simvola p kak "ravno, esli" i simvola q kak "otnyat' iz" v pervonachal'noj pq-sisteme. Hotya eto dovol'no trivial'nyj primer, v etom skryta sut' idei, chto simvoly mogut imet' mnogo smyslovyh interpretacij v zavisimosti ot nablyudatelya, kotoryj ih ustanavlivaet.
Teper' mozhno summirovat' nashi nablyudeniya po povodu slova "neprotivorechivost'". My nachali nashe rassuzhdenie, poluchiv to, chto, kazalos', protivorechit formal'noj sistemoj - vnutrenne protivorechit i protivorechit s vneshnim mirom. No sekundu spustya my vse rasstavili po mestam, kogda obnaruzhili svoyu oshibku: my vybrali neudachnuyu interpretaciyu dlya simvolov. Izmeniv interpretaciyu, my vosstanovili posledovatel'nost' sistemy! Teper' stanovit'sya yasnym. CHto posledovatel'nost' (ili neprotivorechivost') ne yavlyaetsya sobstvennym svojstvom formal'noj sistemy samo po sebe, a zavisit ot interpretacii, kotoruyu predlagayut dlya nee. Iz teh zhe samyh soobrazhenij vyhodit, chto protivorechivost' nesvojstvenna lyuboj formal'noj sisteme.
No eto opredelenie, kazhetsya, govorit otnositel'no protivorechivosti s vneshnim mirom. CHto zhe otnositel'no vnutrennih protivorechij? Vozmozhno, sistema byla by vnutrenne protivorechivoj, esli by ona soderzhala dve ili bolee teoremy, ch'i interpretacii byli nesovmestimy drug s drugom, i vnutrenne posledovatel'na, esli vse interpretiruemye teoremy byli sovmestimy drug s drugom. Rassmotrim, naprimer, formal'nuyu sistemu, imeyushchuyu vsego tri teoremy: TbZ, ZbE, i EbT. Esli T interpretirovat' kak "CHerepaha" Z kak "Zenon", E kak "|gbert", a ' x b y' , interpretirovat', kak "x vsegda pobezhdaet v shahmatah y", to my imeem sleduyushchuyu interpretaciyu teorem:
Zenon vsegda pobezhdaet v shahmatah |gberta.
|gbert vsegda pobezhdaet v shahmatah CHerepahu
Utverzhdeniya ne nesovmestimy, hotya oni opisyvayut dovol'no prichudlivyj krug shahmatistov. Sledovatel'no, v etoj interpretacii, formal'naya sistema, v kotoroj eti tri cepochki simvolov yavlyayutsya teoremami, vnutrenne posledovatel'na, hotya, fakticheski, ni odno iz etih utverzhdenij ne yavlyaetsya istinnym! No vnutrennyaya posledovatel'nost' ne trebuet, chtoby vse teoremy poluchilis' istinnymi. Prosto oni dolzhny byt' sovmestimy drug s drugom.
Teper' predpolozhite vmesto etogo, chto ' x b y' nado interpretirovat', kak "h byl izobreten u".
Togda my imeli by:
Zenon byl izobreten |gbertom.
|gbert byl izobreten CHerepahoj.
V etom sluchae ne imeet znacheniya, yavlyaetsya li kazhdoe otdel'no vzyatoe utverzhdenie istinnym ili net. Vozmozhno, net nikakogo sposoba uznat' kakoe iz nih lozhno, a kakoe - pravda. No v chem mozhno byt', odnako, uverennym, eto v tom, chto ne vse oni mogut byt' istinnymi odnovremenno. Takim obrazom, eta interpretaciya delaet sistemu vnutrenne protivorechivoj. |ta protivorechivost' zavisit ne ot interpretacii etih treh zaglavnyh bukv, no ot interpretacii simvola b i iz fakta, chto eti tri literala ciklicheski perestavleny vokrug svyazki b. Takim obrazom, mozhno obnaruzhit' vnutrennyuyu protivorechivost', ne interpretiruya vse simvoly formal'noj sistemy (v dannom sluchae dostatochno bylo interpretirovat' odin edinstvennyj simvol). K tomu momentu, kogda dostatochno mnogo simvolov uzhe poluchili interpretaciyu, mozhet vyyasnit'sya, chto net nikakogo sposoba, kotorym by ostal'naya chast' simvolov mogla by byt' interpretirovana tak, chtoby vse teoremy poluchilis' istinnymi. No eto ne tol'ko vopros istiny i lzhi - eto vopros vozmozhnostej. Vse tri teoremy vyshli by lozhnymi, esli zaglavnye bukvy interpretirovalis' by kak nazvaniya real'nyh lyudej. No ne v etom prichina, pochemu my nazvali sistemu vnutrenne protivorechivoj. Osnovaniem dlya etogo byli ciklicheskaya zavisimost' simvola b pri takoj interpretacii (Kstati, vy najdete bol'she ob etom treugol'nike avtorov v glave XX).
Gipoteticheskie miry i protivorechivost'
My pokazali dva sposoba smotret' na posledovatel'nost' (neprotivorechivost'): pervyj govorit chto "sistema plyus interpretaciya" soglasuetsya s vneshnim mirom, esli kazhdaya teorema poluchaetsya istinnoj pri interpretacii. Vtoroj sposob govorit, chto "sistema plyus interpretaciya" yavlyaetsya vnutrenne posledovatel'noj, esli vse teoremy poluchat'sya vzaimno sovmestimymi pri interpretacii. Imeetsya blizkaya svyaz' mezhdu etimi dvumya tipami posledovatel'nostej. CHtoby opredelit' yavlyayutsya li nekotorye vyskazyvaniya vzaimno-sovmestimymi, vy probuete predstavit' sebe mir, v kotorom vse oni mogut byt' odnovremenno istinnymi. Poetomu vnutrennyaya neprotivorechivost' zavisit ot neprotivorechivosti s vneshnim mirom tol'ko teper' "vneshnemu miru" pozvoleno byt' lyubym voobrazhaemym mirom, vmesto togo, v kotorom my zhivem. No eto chrezvychajno neopredelennoe i neudovletvoritel'noe reshenie voprosa. CHto predstavlyayut soboj "voobrazhaemye miry"? V konce koncov, mozhno voobrazit' miry, v kotoryh tri personazha ciklicheski izobretayut drug druga. Ili net? Vozmozhno li, izobresti mir, v kotorom imeyutsya kvadratnye krugi? Mozhno li voobrazit' mir, v kotorom pravyat zakony mehaniki N'yutona, a ne otnositel'nost'? Vozmozhno li voobrazit' mir v kotorom zelenoe odnovremenno mozhet byt' ne zelenym? Ili mir, v kotorom zhivotnye sostoyat ne iz kletok? Predstavim li mir, v kotorom Bah improviziruet fugu s vosem'yu chastyami na temu korolya Fridriha Velikogo? A mir, v kotorom moskity yavlyayutsya bolee umnymi, chem lyudi?
Odna formal'naya sistema vnutri drugoj
V predydushchem primere nekotorye simvoly mogli imet' interpretaciyu, v to vremya kak drugie ne imeli. |to napominaet nam ob opisanii geometrii na estestvennom yazyke s ispol'zovaniem nekotoryh slov kak neopredelennyh terminov. V takom sluchae vse slova razdelyayutsya na dva klassa: te, ch'e znachenie ustanovleno i neizmenno i te, kotorye dolzhny byt' utochneny dlya vyyasneniya neprotivorechivosti sistemy (oni - neopredelennye terminy). Postroenie geometrii takim sposobom trebuet, chtoby smysl terminov byl uzhe ustanovlen na bolee vysokom urovne gde-to za predelami geometrii. |ti slova sostavlyayut zhestkij skelet, obrazuyut osnovnoj karkas sistemy, kotoryj potom zapolnyaetsya drugim materialom i kotoryj mozhno, pri zhelanii, zamenit' (Evklidova ili neevklidova geometriya).
Fragmenty stabil'nosti v vizual'nom prostranstve
Podobnym ierarhicheskim sposobom my priobretaem novye znaniya, novye slova, oshchushchaem, chto ob容kt nam neznakom. |to osobenno interesno v sluchae vospriyatiya risunkov |shera, tipa Otnositel'nosti (ris 22), vnutri kotoryh nahodyatsya nevozmozhnye ob容kty. Vy mozhete predstavit' kak my delaem samye raznye interpretacii, davaya inoe tolkovanie kartine raz za razom, poka ne najdem interpretaciyu vseh ee chastej, svobodnuyu ot vzaimnyh protivorechij. No nashi popytki besplodny. My smotrim na eto ozadachennye i udivlennye. My ozadachenny lestnicami, po kazhdoj iz kotoryh dvizhutsya lyudi v napravlenii, protivorechashchih kazhdoj otdel'no vzyatoj lestnice. |ti lestnicy -"ostrova uverennosti" na kotoryh my baziruem nashu interpretaciyu polnoj kartiny. Odnazhdy identificirovav takoj ostrov, my probuem rasshirit' nashe ponimanie, pytayas' ustanovit' otnosheniya, v kotoryh oni nahodyatsya drug k drugu. No v etih popytkah my stalkivayutsya s nepriyatnost'yu.
Esli my sdelaem popytku otstupit', to est' podvergnut' somneniyu "ostrova uverennosti", to my tak zhe stolknemsya s nepriyatnost'yu, no drugogo roda. Net nikakogo sposoba uhvatit'sya za zadnij plana, i prichina etogo oni zhe - lestnicy. Oni ne ryba, ne plet' ne ladon' - oni vsego lish' lestnicy. ( Imeetsya eshche odna vozmozhnost' - ostavit' vse linii na kartine polnost'yu ne interpretirovannymi podobno "bessmyslennym simvolam" formal'noj sistemy. |tot edinstvennyj spasitel'nyj put' i yavlyaetsya primerom U-sposoba. Dzen-podhodom k simvolam)
Mozhno li predstavit' mir, v kotorom cherepahi mogut igrat' fugi ili razgovarivat'?!
CHerepaha, igrayushchaya v futbol, eto bylo by slishkom, konechno. . .
Nekotorye iz etih mirov kazhutsya bolee realistichnymi chem drugie, v to vremya kak nekotorye, kazhetsya, voploshchayut v sebe logicheskie protivorechiya. Naprimer, zelenyj i ne zelenyj. V to vremya kak nekotorye kazhutsya (ne imeya luchshego slova) "veroyatnymi". Tipa togo mira, gde Bah improviziruet fugi iz vos'mi chastej ili mir gde zhivotnye ne sostoyat iz kletok. Ili dazhe, zadumajtes' ob etom, mir, v kotorom zakony fiziki dolzhny byt' drugimi. Grubo govorya, togda dolzhna ustanovit'sya drugie standarty neprotivorechivosti. Naprimer, naibolee myagkoj byla by "logicheskaya posledovatel'nost'", kotoraya ne nakladyvala by na ob容kty nikakih ogranichenij, krome logicheskih. Bolee tochno: "sistema plyus interpretaciya" byla by logicheski posledovatel'ny dlya nas, do teh por, poka lyubaya iz dvuh ee teorem ne protivorechat drug drugu pri interpretacii, matematicheski posledovatel'ny do teh por, poka interpretiruemye teoremy ne narushayut matematiku, fizicheski posledovatel'ny poka interpretiruemye teoremy sovmestimy s zakonami fiziki. Za etim sleduyut biologicheskaya neprotivorechivost' i tak dalee. V biologicheski posledovatel'noj sisteme imelis' by teorema, ch'ya interpretaciya glasila by "SHekspir napisal operu" no ne soderzhala by nikakoj teoremy, interpretaciya kotoroj glasila: "sushchestvuyut zhivotnye men'she kletki". Voobshche govorya, takogo roda fantasticheskaya protivorechivost' ne izuchayutsya po prichine nevoobrazimoj hitrospletennosti urovnej utverzhdenij. Kakaya protivorechivost', naprimer, mozhno skazat', voznikaet v probleme treh personazhej, gde neyasno kto kogo izobretaet?
Logicheskaya? Fizicheskaya? Biologicheskaya? Literaturnaya?
Obychno granica mezhdu interesnoj i neinteresnoj oblast'yu prolegayut mezhdu fizicheskoj i matematicheskoj neprotivorechivost'yu (konechno, matematiki i logiki, kotorye ee provodyat, vryad li bespristrastnaya sudejskaya komanda. . ..) |to znachit, chto vidy protivorechij, kotorye "uchityvayutsya" dlya formal'nyh sistem, yavlyat'sya tol'ko logicheskogo i matematicheskogo tipa. No i po etomu soglasheniyu my vse zhe nashli interpretaciyu, kotoraya delaet trio teorem TbZ, ZbE, EbT protivorechivym. My mozhem delat' takuyu interpretaciyu dlya b : "yavlyaetsya bol'she chem". CHto mozhno skazat' v otnoshenii T, Z i E? Oni mogut interpretirovat'sya kak natural'nye chisla, naprimer Z kak 0, T kak 2 i E kak 11. Zamet'te, chto dve teoremy poluchat'sya v etom sluchae istinnymi, a odna - lozhnaya. Esli by my vmesto etogo interpretirovali Z kak 3, to my imeli by dva lozhnyh vyskazyvaniya i tol'ko odno istinnoe. No v lyubom sluchae my imeli by protivorechie. Fakticheski, znacheniya, prisvoennye T, Z i E neprimenimy (nerelevantnye) poka my podrazumevaem pod nimi tol'ko natural'nye chisla. V ocherednoj raz my vidim, chto neobhodima tol'ko chast' interpretacii, chtoby priznat' vnutrennyuyu protivorechivost'.
Formal'nye sistemy chasto vystraivayutsya imenno v takoj ierarhicheskoj ili uporyadochennoj manere. Naprimer, Formal'naya Sistema I mogla by byt' vystroena s pravilami i aksiomami, kotorye dayut uverennost' predpolagat' passivnoe znachenie ee simvolov. Teper', dopustim Formal'naya, Sistema I. vklyuchaetsya polnost'yu v bol'shuyu sistemu, sistemu s bol''shim kolichestvom simvolov - Formal'nuyu sistemu II. Togda pravila i aksiomy Formal'noj Sistemy I yavlyayutsya chast'yu pravil i aksiom Formal'noj sistemy II. Passivnoe znachenie simvolov Formal'noj Sistemy I ostaetsya dejstvitel'nymi, ostayutsya ee formoj i neizmennym skeletom, kotoryj igraet bol'shuyu rol' v opredelenii passivnogo smysla (znacheniya) novyh simvolov v Formal'noj Sisteme II. Vtoraya sistema, v svoyu ochered', mozhet sluzhit' skeletom tret'ej sisteme i tak dalee. |to vpolne vozmozhno i geometriya - horoshij etomu primer. Imet'sya sistema (ta zhe, Absolyutnaya geometriya) kotoraya chastichno vyyavlyaet passivnoe znachenie neopredelennyh terminov, a nekotorye drugie mogut byt' dobavleny dopolnitel'nymi pravilami i aksiomami, kotorye v dal'nejshem ogranichivayut passivnye znacheniya neopredelennyh terminov. Vse proishodit tak, kak proishodit s evklidovoj i neevklidovoj geometriej.

Ris. 22 Otnositel'nost', M. C. Escher (lithograph, 1953).
V itoge my vynuzhdeny po ierarhicheskomu harakteru nashego processa myshleniya videt' ili sumasshedshij mir ili tol'ko spletenie bessmyslennyh linij. Podobnyj analiz mozhno bylo by sdelat' dlya mnogih kartin |shera, kotorye opirayutsya na predstavleniya nekotoryh osnovnyh form, raspolozhennyh nestandartnym obrazom i nablyudatel' vidit paradoks na vysokom urovne. No otstupat' uzhe slishkom pozdno. On ne mozhet vernut'sya i izmenit' svoe mnenie otnositel'no togo, kak interpretirovat' ob容kty nizshego urovnya. Razlichie mezhdu risunkami |shera i neevklidovoj geometriej to, chto v geometrii razumnaya interpretaciya mozhet byt' najdena dlya neopredelennyh terminov v rezul'tate postizheniya vsej sistemy, v to vremya, kak dlya tvorenij |shera okonchatel'nyj vyvod ne sovmestim ni s kakoj vozmozhnoj real'nost'yu, nezavisimo ot togo kak dolgo kazhdyj budet smotret' na kartinu. Konechno, mozhno vse eshche vydumyvat' fantasticheskie miry v kotoryh |sherovskie tryuki mogut proishodit'. . . No v takih mirah zakony biologii, fiziki, matematiki ili dazhe logiki budut narusheny na odnom urovne v to vremya kak na drugom oni prodolzhayut spokojno ispolnyat'sya, chto pridaet etim miram krajnyuyu sverh容stestvennost' (Primer etogo - Vodopad (ris5) , gde normal'noe tyagotenie dejstvuet na peremeshchenie vody, no priroda prostranstva narushena)
Odinakova li matematika v lyubom iz myslimyh mirov?
Tol'ko chto my podcherknuli izlozhennyj vyshe fakt, chto vnutrennyaya neprotivorechivost' formal'noj sistemy (vmeste s interpretaciej) trebuet chtoby imelsya nekotoryj voobrazimyj mir gde eto vozmozhno, to est' mir, ogranichennyj tol'ko tem, chto matematika i logika v nem takie zhe samye, kak i v nashem mire. V takom mire vse interpretiruemye teoremy dolzhny byt' istinnymi. Vneshnyaya neprotivorechivost', odnako (posledovatel'nost' s vneshnim mirom) trebuet, chtoby vse teoremy vyshli istinnymi v real'nom mire. V osobom sluchae, kogda est' zhelanie vystroit' posledovatel'nuyu sistemu, ch'i teoremy dolzhny interpretirovat'sya tol'ko kak utverzhdeniya matematiki, to kazalas' by, chto razlichie mezhdu dvumya tipami posledovatel'nosti dolzhny ischeznut'. S etogo momenta, soglasno tomu, chto my skazali, vse voobrazhaemye miry imeyut tu zhe matematiku chto i real'nyj mir. V kazhdom myslimom mire 1 plyus 1 dolzhno ravnyat'sya 2, analogichno dolzhno imet'sya beskonechnoe chislo prostyh chisel. Krome togo, v kazhdom iz myslimyh mirov, pryamye ugly dolzhny sovpadat', i konechno cherez lyubuyu tochku ne na dannoj linii mozhno provesti odnu i tol'ko odnu parallel'nuyu liniyu...
YAvlyaetsya li teoriya chisel odnoj i toj zhe vo vseh myslimyh mirah?
Esli my predpolagaem chto logika dolzhna byt' neot容mlemoj chast'yu lyubogo voobrazhaemogo nami mira (i obratite vnimaniya, my ne imeem v vidu kakuyu-to dvojnuyu logiku, no v sleduyushchih glavah my vstretim i eto) to chto iz etogo? Dejstvitel'no li mozhno predstavit', chto v nekotoryh iz mirov net beskonechnogo chisla prostyh chisel? Kazhetsya li stol' neobhodimymi, chtoby chisla povinovalis' odnim i tem zhe zakonam vo vseh myslimyh mirah? Ili o koncepcii "natural'noe chislo" luchshe dumat' kak o neopredelennom termine podobno "TOCHKA" ili "PRYAMAYA"? V etom sluchae teoriya chisel byla by bifurkacionnoj (razvetvlyayushchejsya) teoriej . Podobno geometrii imelis' by standartnye i nestandartnye teorii chisel. No togda dolzhen byl by sushchestvovat' nekij analog absolyutnoj geometrii: "bazovaya" teoriya, invariantnyj komponent vseh teorij chisel, kotoraya by identificirovala by kazhduyu teoriyu kak teoriyu chisel v bol'shej stepeni, chem skazhem teoriyu bananov ili kauchuka. V nastoyashchij moment, kazhetsya, dostignuto soglasie sovremennyh matematikov i filosofov, chto imeetsya takaya teoriya chisel, kotoruyu naryadu s logikoj nuzhno by vklyuchit' v to, chto my podrazumevaem pod "myslimymi mirami". |to yadro teorii chisel, analogiya absolyutnoj geometrii, nazyvaetsya arifmetikoj Peano (Peano) i my formalizuem ee v glave VIII. Tak zhe ( eto teper' horosho ustanovleno kak sledstvie teoremy Gedelya) teoriya chisel dejstvitel'no yavlyaetsya bifurkacionnoj teoriej so standartnymi i nestandartnymi versiyami. No v otlichii ot situacii v geometrii, chislo "tipov" teorij chisel beskonechno, chto delaet situacii znachitel'no slozhnee.
Polnota
Esli posledovatel'nost' ili neprotivorechivost' -minimal'noe uslovie pri kotorom simvoly priobretayut passivnyj smysl, to dopolnyayushchim ego ponyatiem yavlyaetsya polnota, kotoraya yavlyaetsya polnym i okonchatel'nym podtverzhdeniem passivnogo smysla simvolov. Esli neprotivorechivost' - eto svojstvo togo, chto "vse chto proizvoditsya sistemoj istinno", to polnota govorit o drugom: "kazhdoe istinnoe utverzhdenie proizvoditsya vnutri sistemy"
Primer formal'noj sistemy, kotoraya yavlyaetsya polnoj na skromnom urovne - pervonachal'naya pq-sistema s pervonachal'noj interpretaciej. Vse istinnye utverzhdeniya o summah dvuh polozhitel'nyh celyh chisel predstavleny teoremami sistemy. My mogli by skazat' eto po-drugomu: "Istinnost' vseh utverzhdenij o znachenii summy dvuh polozhitel'nyh celyh chisel my dokazyvaem v predelah sistemy". (Vnimanie! Kogda my nachinaem ispol'zovat' termin "dokazyvaemoe utverzhdenie" vmesto "teorema", eto pokazyvaet, chto my nachinaem stirat' razlichie mezhu formal'noj sistemoj i ee interpretaciej. |to normal'no, esli my horosho osoznaem tumannost' termina, i pri uslovii, chto my ponimaem, chto inogda vozmozhny raznye interpretacii). Pq-sistema v pervonachal'noj interpretacii polna. Ona tak zhe neprotivorechiva (posledovatel'na), tak kak nikakoe lozhnoe utverzhdenie (ispol'zuya nashu novuyu frazu) ne dokazuemo v predelah sistemy.
Kak interpretaciya razrushaet ili vosstanavlivaet polnotu
CHto ya imel v vidu, kogda govoril, chto "polnota eto polnoe i okonchatel'noe podtverzhdenie passivnogo smysla"? |to oznachaet, chto esli sistema postroena, no ona nepolna, to imeetsya nesootvetstvie mezhdu simvolami i ih interpretaciej. Sistema ne imeet moshchnosti opravdat' sebya, buduchi interpretirovana takim obrazom. Inogda, esli interpretaciya nemnogo "urezana", sistema mozhet stat' polnoj. CHtoby illyustrirovat' etu ideyu, davajte posmotrim na izmenennuyu pq-sistemu (ispol'zuyushchuyu vtoruyu shemu aksiom) i ee novuyu interpretaciyu, kotoruyu my primenili dlya nee.
Nepolnota formal'noj teorii chisel
V teorii chisel my stolknemsya s nepolnotoj snova. No tam, chtoby ispravit' situaciyu, nas budut vlech' v druguyu storonu - k dobavleniyu novyh pravil, to est' my budem stremit'sya sdelat' sistemu eshche bolee moshchnoj. Ironiya v tom, chto vsyakij raz, kogda my dobavlyaem novye pravila, my dumaem, chto vot teper' uzhe my sdelaem sistemu polnoj. I harakter dannogo bezvyhodnogo polozheniya mozhno illyustrirovat' sleduyushchej allegoriej. . .
No minutochku! No eto zhe postulat o parallel'nyh i utverzhdat', chto on universalen bylo by oshibkoj v svyazi s tem, chto my uzhe znaem. Esli vse voobrazhaemye miry povinuyutsya postulatu o parallel'nyh, to tem samym my utverzhdaem chto neevklidova geometriya nevozmozhna. |to vozvrashchaet nas nazad, k tem zhe predstavleniyam chto ispovedovali Sakcheri i Lambert. |to neblagorazumno. No chto zhe poluchaetsya? Ne vsya matematika odinakova v lyubom iz myslimyh mirov? A mozhet pod podozreniem i sama logika? Predstavimy li miry, gde protivorechiya - norma sushchestvovaniya? Miry, gde protivorechie- ne protivorechiya?
Horosho. V nekotorom smysle, prosto fantaziruya, my pokazali chto takie miry yavlyayutsya dejstvitel'no myslimymi, no v bolee glubokom smysle oni vse zhe ochen' nevoobrazimy ( eto samo po sebe nebol'shoe protivorechie). Ves'ma vazhnym, odnako, predstavlyaetsya sleduyushchee: esli my hotim imet' vozmozhnost' svyazat' voedino vse v nashem voobrazhaemom mire, my dolzhny prinyat' nekotoruyu obshchuyu osnovu i eto dolzhno izryadno vklyuchat' logiku. (Imeyutsya sistemy veroispovedaniya, kotorye otklonyayut takuyu tochku zreniya, pologaya ee slishkom logicheskoj. V chastnosti, Zen vklyuchaet v sebya kak protivorechiya, tak i neprotivorechivye fakty v ravnoj mere. |to mozhet kazat'sya neposledovatel'nym (protivorechivym), no esli neposledovatel'nost' tozhe chast' veroispovedaniya, to chto mozhno eshche vozrazit'?)
Dlya prakticheskogo ispol'zovaniya vse teorii chisel - odinakovye. Drugimi slovami, esli by stroitel'stvo mosta zaviselo ot teorii chisel (chto v nekotorom smysle tak i est'), to fakt, chto imeyutsya razlichnye teorii chisel, ne imel by znacheniya, tak kak aspekty otnosyashchiesya k real'nomu miru vo vseh teoriyah chisel sovpadayut drug s drugom. Nel'zya skazat' togo zhe samogo otnositel'no razlichnyh geometrij. Naprimer, summa uglov treugol'nika 180 gradusov tol'ko v Evklidovoj geometrii, no ona bol'she v ellipticheskoj geometrii i men'she v giperbolicheskoj. Izvestno, chto odnazhdy Gauss popytalsya izmerit' summu uglov v bol'shom treugol'nike, mezhdu tremya vershinami gor chtoby raz i na vsegda opredelit' kakogo vida geometriya v dejstvitel'nosti carit v nashej vselennoj. Spustya sto let |jnshtejn sozdal Obshchuyu Teoriyu Otnositel'nosti, kotoraya utverzhdala, chto geometriya vselennoj opredelyaetsya soderzhashchejsya v nej materiej. Tak chto nikakaya konkretno geometriya ne svojstvenna prostranstvu neposredstvenno. Na vopros "Kakaya geometriya yavlyaetsya istinnoj?" priroda daet neodnoznachnyj otvet ne tol'ko v matematike, no i v fizike. CHto zhe kasaetsya voprosa "Kakaya teoriya chisel yavlyaetsya istinnoj?" to my smozhem ob etom govorit' bol'she, posle prohozhdeniya Teoremy Gedelya podrobno.
Poyasnim eti ponyatiya. My ne podrazumevaem (i ne mozhem podrazumevat') kazhdoe istinnoe utverzhdenie v mire. My podrazumevaem tol'ko te, kotorye prinadlezhat oblasti, kotoruyu pytaemsya predstavit' v sisteme. Poetomu polnota oznachaet:
"Kazhdoe istinnoe utverzhdenie, kotoroe mozhet byt' vyrazheno nekotoroj zapis'yu s pomoshch'yu simvolov sistemy - teorema sistemy".
Neprotivorechivost': kogda kazhdaya teorema pri interpretacii okazyvaetsya istinnoj (v nekotorom voobrazhaemom mire).
Polnota: kogda vse utverzhdeniya, kotorye yavlyayutsya istinnymi (v nekotorom voobrazhaemom mire) mogut byt' vyrazheny v vide cepochek simvolov sistemy i yavlyayutsya teoremami.
Kto-to mog by utverzhdat', chto eta sistema, mol, ne polna na osnovanii togo, chto summa treh polozhitel'nyh celyh chisel (tipa 2+3+4 =9) ne predstavlyaetsya teoremami pq-sistemy, hotya ona predstavima v notacii sistemy (naprimer: _ _ p _ _ _ p _ _ _ _ q _ _ _ _ _ _ _ _ _). Odnako eta cepochka nepravil'no postroena i sledovatel'no dolzhna rassmatrivat'sya kak absolyutno bessmyslennaya nastol'ko, naskol'ko bessmyslenna cepochka _ pqp _ _ _ qpq . Trojnaya summa prosto ne vyrazhaetsya v notacii sistemy, tak chto polnota sistemy sohranyaetsya.
Nesmotrya na polnotu pq-sistemy v etoj interpretacii, ona, konechno, slishkom daleka ot okonchatel'nogo zavoevaniya vsej istiny v teorii chisel. Naprimer, ne imeetsya nikakogo sposoba, kakim by pq-sistema soobshchila nam, skol'ko sushchestvuet prostyh chisel. Teorema Gedelya o nepolnote govorit, chto lyubaya sistema, kotoraya yavlyaetsya "dostatochno moshchnoj", imenno iz za svoej moshchi yavlyaetsya nepolnoj. |to znachit, chto tam est' pravil'no postroennye cepochki, kotorye vyrazhayut istinnye utverzhdeniya teorii chisel, no kotorye ne yavlyayutsya teoremami ( imeyutsya istiny v teorii chisel, kotorye ne dokazuemy v predelah sistemy). Sistemy, podobnye pq-sisteme, yavlyayutsya polnymi, no ne ochen' moshchnymi. Oni chto-to napodobie fonografov s nizkim kachestvom zvuchaniya. |ti sistemy nastol'ko bedny iznachal'no, chto stanovit'sya ochevidnym: oni ne mogut nas udovletvorit', oni ne mogut soobshchit' nam vse, chto my hoteli by znat' otnositel'no teorii chisel.
Posle izmeneniya pq-sistemy my izmenili i interpretaciyu dlya q s "ravnyaetsya" na "bol'she chem ili rovno". My vidim, chto izmenennaya pq-sistema byla posledovatel'na v takoj interpretacii i vse zhe chto-to zdes' ne tak. Problema prosta: imeetsya teper' mnogo vyrazhennyh v notacii sistemy istin, kotorye okazyvayutsya ne teoremami. Naprimer "2 plyus 3 bol'she chem ili ravno 1" vyrazheno ne teoremoj _ _ p _ _ _ q _ . Interpretaciya slishkom svobodnaya! Ona ne ochen' akkuratno otobrazhaet to, chto teoremy delayut v sisteme. V takoj shirokoj interpretacii pq-sistema nepolna. My mogli by vosstanovit' situaciyu ili (1) dobavleniem novye pravil k sisteme, delaya ee bolee moshchnoj ili (2) suziv interpretaciyu. V etom smysle razumnym kazhetsya vybrat' vtoroj put' - uzhat' interpretaciyu. Vmesto interpretacii q "bol'she chem ili ravno". My dolzhny ispol'zovat' "ravnyaetsya ili bol'she na 1". Teper' sistema stanovit'sya i posledovatel'noj i polnoj. I polnota podtverzhdaet spravedlivost' (umestnost') interpretacii.
Vy imeete proigryvatel' i imeete gramzapis', kotoraya, v poryadke rabochej gipotezy, pomechena kak "Kanon B-A-C-H". Odnako, kogda my igraem etu gramzapis' na proigryvatele, vynuzhdennye obratnoj svyaz'yu kolebaniya (kak eto sluchalos' s zapisyami CHerepahi) vmeshivayutsya nastol'ko sil'no, chto my ne mozhem ulovit' na fone etih pomeh melodiyu. Togda my prihodim k zaklyucheniyu, chto chto-to iz dvuh defektnoe. Ili nasha gramzapis' ili nash proigryvatel'. CHto by proverit' nashu gramzapis', my dolzhny proslushat' ee na proigryvatele druzej i uslyshat' kachestvo zvuchaniya. CHtoby proverit' proigryvatel', my dolzhny postavit' na nego kakuyu-libo gramzapisi druzej i ubedit'sya sootvetstvuet li zvuchanie tomu, chto napisano na etiketke. Esli nash proigryvatel' projdet eto ispytanie, to my skazhem, chto gramzapis' defektna. Naoborot, esli gramzapis' projdet ispytanie, to my skazhem, chto proigryvatel' defektnyj. No chto my mozhem skazat', esli oba projdut sootvetstvuyushchie ispytaniya? V etom sluchae stoit vspomnit' cep' dvuh izomorfizmov (ris. 20) i tshchatel'no dumat'!
[ predydushchaya ][ oglavlenie ]
Sopyleft © A Semenov 2002
[ vverh ]