GEB
Duglas R. Hofshtadter.
[ predydushchaya ] [ oglavlenie ] [ sleduyushchaya ]

Perevod Aleksandra Semenova

G L A V A   III
Figura i Fon

Prostye chisla protiv sostavnyh

Est' chto-to strannoe v idee, chto mysl', vo vsem svoem mnogoobrazii, mozhet byt' vosproizvedena prostymi tipografskimi manipulyaciyami. Edinstvennaya poka nami udachno vosproizvedennaya takim obrazom ideya - eto ideya summirovaniya, i v etom net nichego strannogo. No predpolozhim, chto nasha cel' - sozdat' formal'nuyu sistemu s teoremami formy Px gde simvol x - eto cepochka defisov i teoremami byli by tol'ko te cepochki, u kotoryh kolichestvo defisov - prostoe chislo. To est' P_ _ _ byla by teoremoj, a P_ _ _ _ - net. Kak eto mozhno bylo by sdelat' tipografskimi sposobom?
Snachala, vazhno chetko opredelit', chto my ponimaem pod tipografskimi dejstviyami. Polnyj nabor takih dejstvij my mogli videt' v MIU-sisteme i pq-sisteme, tak chto nam tol'ko ostalos' privesti spisok etih dejstvij:

    (1)  chitat' i raspoznavat' lyuboj simvol iz konechnogo mnozhestva (alfavita);
    (2)  pisat' lyuboj simvol, prinadlezhashchij k etomu mnozhestvu;
    (3)  kopirovat' lyuboj iz etih simvolov iz odnogo mesta v drugoe;
    (4)  stirat' lyuboj iz vybrannyh simvolov;
    (5)  sravnivat' dva simvola, stoyashchie v raznyh mestah;
    (6)  hranit' i ispol'zovat' spisok ranee proizvedennyh teorem.

|tot spisok nemnogo izbytochen, no eto ne vazhno. Vazhno, chto zdes' yasno vidno - ispol'zuyutsya tol'ko elementarnye vozmozhnosti. Kazhdaya iz nih gorazdo proshche, chem sposobnost' otlichit' prostoe chislo ot sostavnogo. Kak zhe togda my mozhem skombinirovat' nekotorye iz etih dejstvij, chtoby postroit' formal'nuyu sistemu, kotoraya razdelyaet prostye chisla ot sostavnyh?

Tp-sistema

Pervym shagom k dostizheniyu etoj celi mozhet stat' reshenie bolee prostoj, no svyazannoj s etim zadachi. My mozhem poprobovat' sdelat' sistemu, podobnuyu pq-sisteme, za isklyucheniem togo, chto v nej otobrazhaetsya umnozhenie, a ne slozhenie. Davajte nazovem ee Tq-sistemoj, t - 'times' - kratnost'. Bolee opredelenno: predpolozhim X, Y i Z - eto sootvetstvenno chislo defisov v x, y i z - cepochkah iz defisov. (Zamet'te. YA ispol'zuyu razlichnoe napisanie dlya togo, chtoby otlichit' chislo defisov v cepochkah i naimenovanie samih cepochek.) Togda my priznaem cepochku x t y q z teoremoj, esli X, umnozhennoe na Y, ravnyaetsya Z. Naprimer _ _ t _ _ _ p _ _ _ _ _ _ dolzhna byt' teoremoj, tak kak 2 umnozhennoe na 3 daet 6. No _ _ t _ _ _ p _ _ _ ne dolzhna byt' teoremoj. Tp-sistema mozhet byt' opisana primerno tak zhe legko, kak i pq-sistema, a imenno: ispol'zuya tol'ko odnu shemu aksiom i tol'ko odno pravilo vyvoda:

    Shema aksiom: x t _ q x aksioma, vsyakij raz, kogda x -cepochka defisov.
    Pravilo vyvoda: predpolozhim, chto x, y i z - kakie-to cepochki defisov. I predpolozhim, chto x t y q z -staraya teorema. Togda x t y _ q zx - novaya teorema.
Nizhe pokazan vyvod teoremy _ _ t _ _ _ p _ _ _ _ _ _

(1) _ _t _ q _ _ .....................(Aksioma)
(2) _ _ t_ _ q _ _ _ _ ........... (Po pravilu vyvoda, ispol'zuya (1) kak staruyu teoremu)
(3) _ _ t_ _ _ q _ _ _ _ _ _ .. (Po pravilu vyvoda, ispol'zuya (2) kak staruyu teoremu)

Obratite vnimanie - srednyaya cepochka defisov uvelichivaetsya na odin defis pri kazhdom primenenii pravila vyvoda, poetomu legko predskazat', chto esli vy hotite poluchit' teoremu s 10-yu defisami v seredine, to vy primenite pravilo vyvoda devyat' raz podryad.

Pokorenie slozhnyh

Teper' i umnozhenie (neskol'ko bolee hitraya ideya, chem slozhenie) tozhe "pojmana" v seti tipografskih simvolov podobno pticam na gravyure |shera "Osvobozhdenii". Nu a chto zhe s prostymi chislami? U nas est' plan, kotoryj kazhetsya blestyashchim: ispol'zuya tp-sistemu opredelit' novoe mnozhestvo teorem formy Cx , kotorye harakterizuyut sostavnye (slozhnye) chisla sleduyushchim obrazom:

    Pravilo: predpolozhim, chto x, y i z - kakie-to cepochki defisov. Esli x_ t y_ q z - teorema. Togda Cz -teorema.

|to srabotaet vot pochemu. CHislo Z (chislo defisov v cepochke z) yavlyaetsya sostavnym, esli ono est' proizvedenie dvuh chisel bol'shih chem 1, a imenno X+1 (chislo defisov v cepochke x_ ) i Y+1 (chislo defisov v cepochke y_ ). YA otstaivayu pered vami eto novoe pravilo i dlya etogo privozhu v opravdanie "Intellektual'nyj sposob". |to potomu chto vy - chelovek i hotite znat' pochemu poyavilos' takoe pravilo. Rabotaj vy isklyuchitel'no v "Mehanicheskom rezhime", vam ne nuzhny byli by podobnye opravdanii, tak kak v M-rezhime vy mehanicheski sleduete pravilam, schaslivy etim i nikogda ne stanite podvergaya sami pravila somneniyu!

Poskol'ku vy rabotaet v I-rezhime, vy budete vse vremya stremit'sya stirat' v vashem soznanii raznicu mezhdu cepochkami i ih interpretaciyami. Zdes' vy vidite, chto sut' proishodyashchego mozhet okazat'sya ves'ma zaputannoj, esli vy nachinaete chuvstvovat' "smysl" v simvolah, kotorymi manipuliruete. Pridetsya borot'sya s soboj, postoyanno uderzhat' sebya ot mysli, mol, cepochka '_ _ _' yavlyaetsya chislom 3. Trebovanie formal'nosti, kotoroe po nachalu v glave I ozadachivalo (potomu chto ego trebovaniya kazalis' sovershenno ochevidnym) zdes' proyavlyaet svoyu utonchennost' i stanovitsya klyuchevym. |to ochen' vazhnaya veshch' - osteregat'sya smeshivaniya I-sposoba s M-sposobom, inache govorya, vy dolzhny izbegat' soblazna i ne smeshivat' arifmeticheskie fakty s tipografskimi teoremami.

Oshibka v opredelenii prostyh chisel

Ochen' soblaznitel'no pereskochit' srazu ot teorem C-tipa neposredstvenno k teoremam P-tipa, predlozhiv pravilo sleduyushchego vida:

    Predlozhennoe pravilo: Predpolozhim, chto x -cepochka defisov. Togda esli Cx ne teorema, togda Px -teorema.

Fatal'nyj porok etoj idei v tom, chto proverka Cx na prinadlezhnost' k ne teoremam - yavno ne tipografskoe dejstvie. CHtoby znat', chto MU ne teorema MUI-sistemy vy dolzhny vyjti iz sistemy. . . i tochno tak zhe pridetsya postupit' dlya realizacii Predlozhennogo pravila! |to pravilo narushaet vse kanony formal'nyh sistem, ono vynuzhdaet vas rabotat' neformal'no, to est' vne sistemy. Konechno, ranee privedennoe tipografskoe dejstvie (6) pozvolyaet issledovat' zapas ranee najdennyh teorem. No Predlozhennoe pravilo prosit, chto by vy issledovali gipoteticheskuyu "Tablicu Ne-teorem". No chto by poluchit' takuyu tablicu vy byli by dolzhny delat' nekotorye rassuzhdeniya vne sistemy. Stroit' rassuzhdeniya, kotorye pokazali by, pochemu nekotorye cepochki ne mogut byt' polucheny vnutri sistemy. Bylo by ochen' neploho, esli by imelas' drugaya formal'naya sistema, kotoraya mozhet proizvesti "Tablicu ne-teorem" tipografskimi sposobom. Fakticheski nasha cel' i sostoit v tom, chtoby najti imenno takuyu sistemu. No predlozhennoe pravilo - ne tipografskoe pravilo i dolzhno byt' otbrosheno.

|to nastol'ko vazhnyj moment, chto my mogli by na nem ostanovit'sya neskol'ko dol'she. V nashej C-sisteme (kotoraya vklyuchaet Tp-sistemu i pravilo, kotoroe opredelyaet teoremy C-tipa) my imeem teoremy tipa Cx gde 'h' kak obychno - cepochka defisov. Imeyutsya tak zhe ne teoremy formy Cx (oni i est' to, chto ya nazyvayu "ne-teoremam", hotya konechno tt_Cqq i drugoj ploho formalizovannyj musor- ne-teoremy tozhe). Razlichie v tom, chto teoremy imeyut sostavnoe chislo defisov, a ne-teoremy - soderzhat prostoe chislo defisov. Teper' dopustim chto vse teoremy imeyut obshchuyu "formu" (to est' proishodyat iz obshchego nabora tipografskih pravil). Togda i vse ne-teoremy tozhe imeyut obshchuyu "formu" v tom zhe samom smysle? Nizhe priveden spisok teorem C-tipa, pokazannyh bez ih proishozhdeniya. CHisla v skobkah - prosto chislo defisov v teoremah. 

                    C - - - - (4)
                    C - - - - - - (6)
                    C - - - - - - - - (8)
                    C - - - - - - - - - (9)
                    C - - - - - - - - - - (10)
                    C - - - - - - - - - - - - (12)
                    C - - - - - - - - - - - - - - (14)
                    C - - - - - - - - - - - - - - - (15)
                    C - - - - - - - - - - - - - - - - (16)
                    C - - - - - - - - - - - - - - - - - - (18)
                                        *
                                        *
                                        *

"Dyry" v etom spiske i predstavlyayut soboj "ne-teoremy". Povtorim ranee zadannyj vopros: "dyry", v celom, tak zhe imeyut formu? Naskol'ko razumno govorit' lish' na osnovanii togo, chto oni yavlyayutsya propuskami v spiske, mol, oni imeyut nekuyu obshchuyu dlya vseh formu? I da, i net. To, chto oni imeyut nekotorye obshchie tipografskie svojstva - bessporno, no hotim li my nazvat' eto "forma" - ne yasno. Povodom dlya kolebanij yavlyaetsya to, chto "dyry" tol'ko otricatel'no (negativno) opredeleny. Oni - to, chto ostalis' ot spiska, kotoryj byl polozhitel'no (pozitivno) opredelen.

Figura i Fon

Zdes' stoit vspomnit' razlichie mezhdu figuroj i fonom v iskusstve. Kogda figura ili "polozhitel'noe prostranstvo" (naprimer portret cheloveka, zhivopis', natyurmort) narisovany vnutri ramki, neizbezhnym sledstviem stanovit'sya to, chto ego dopolnitel'naya forma( "zadnij plan", "fon", "otricatel'noe prostranstvo") tozhe okazyvaetsya prorisovana. V bol'shinstve kartin otnoshenie figura-fon igrayut otnositel'no nebol'shuyu rol'. Hudozhniki namnogo men'she udelyayut vnimanie fonu, chem figure. No inogda hudozhniki interesuyutsya i fonom tozhe.

Sushchestvuyut krasivye alfavity, kotorye postroeny na igre mezhdu figuroj i fonom. Nizhe privedeno soobshchenie, napisannoe v takom alfavite. Snachala eto poslanie napominaet nagromozhdenie sluchajnyh kapel'. No esli vy rassmatrivaete risunok izdaleka nekotoroe vremya, to vnezapno pered vami vozniknut sem' bukv.


Ris. 15

Podobnyj zhe effekt mozhno uvidet', esli posmotret' na moj risunok Dymovogo Signala (ris. 139). Po nagromozhdeniyu linij otgadajte zagadku: vy mozhete kak-nibud' vydelit' kontur, soderzhashchij slova i v figure, i v fone?

Pozvol'te mne teper' special'no razdelit' dva vida form: kursivno prorisovannye i rekursivnye. (mezhdu prochim, eto moi sobstvennye terminy i zdes' oni ispol'zuyutsya ne sovsem v obychnom smysle). Kursivno prorisovannye figury te, chej fon - sluchajnyj, pobochnyj rezul'tat akta risovaniya. Rekursivnaya figura - ta, chej fon mozhet byt' zamechen kak samostoyatel'naya figura. Obychno takoe vospriyatie prednamerenno provociruetsya hudozhnikom. "Re" v nazvanii "rekursivnyj" oznachaet, chto i perednij plan i fon yavlyayutsya kursivnym risunkom. Figura kak by dvazhdy-kursivna. Kazhdaya granica v rekursivnom risunke - oboyudoostryj mech. M. K. |sher byl masterom v risovanii rekursivnyh figur. Posmotrite, naprimer, na ego prekrasnoe izobrazhenie rekursivnyh ptic (ris 16).

Ris. 16 Ptency v polete opirayutsya na ptencov
M. C. Escher ( 1942 iz zapisnoj knizhki)

No prinyataya nami klassifikaciya izobrazhenij ne stol' strogo kak v matematike. Kto mozhet okonchatel'no skazat', chto lyuboj specificheskij fon ne est' figura? Odnazhdy prorisovannyj, prakticheski vsyakij fon predstavlyaet interes sam po sebe. V etom smysle kazhdaya figura rekursivna. No eto ne to, chto ya vkladyval v smysl etogo termina. U nas imeetsya intuitivnoe, estestvennoe predstavlenie dlya vosprinimaemyh nami form. YAvlyaetsya li i perednij plan, i fon raspoznavaemymi formami? Esli tak, to risunok rekursiven. Esli vy budete vglyadyvat'sya v fona bol'shinstva kartin vy najdete ih dovol'no neuznavaemym. |to znachit:

    Sushchestvuyut raspoznavaemye figury, ch'e otricatel'noe prostranstvo ne yavlyaetsya raspoznavaemoj formoj.
Bolee tehnicheski eto zvuchit tak:

Sushchestvuyut kursivnye formy, kotorye ne rekursivny.

Ideya golovolomki Skotta Kirna (Scott E Kirn) pohozha na ranee upomyanutuyu golovolomku, i ya nazval ee "FIGURO-FIGURNAYA FIGURA". Ona pokazano na ris. 17
Esli vy nastroites' na vospriyatie formy chernogo i belogo odnovremenno, vy budite videt' "FORMU" vsyudu, a "FONA" nigde net! |to primer rekursivnoj figury. V etom hitrom risunke est' dva ne ekvivalentnyh sposoba vosprinimat' chernye oblasti:

Ris. 17 FIGURO-FIGURNAYA FIGURA. Skott Kirn. ( 1975 Scott E Kirn )

    (1) Kak otricatel'noe prostranstvo k belym oblastyam (formam) na risunke.
    (2) Kak transformirovannaya kopiya belyh oblastej (belye oblasti kak by okrasili v chernyj cvet i smestili na shag shiriny po gorizontali)

(V dannom, osobom sluchae "Figurno-figurnoj figury" eti dva sposoba okazalis' ekvivalentny. No v bol'shinstve cherno-belyh kartin etogo ne proizoshlo by). Dalee, v glave VIII, kogda my sozdadim nashu Tipografskuyu Teoriyu CHisel. (TNT - Typographical Number Theory) my budem nadeyat'sya, chto mnozhestvo vseh lozhnyh utverzhdenij teorii chisel mozhet byt' polucheno dvumya analogichnymi sposobami:

    (1) Kak otricatel'noe prostranstvo k mnozhestvu vseh TNT-teorem.
    (2) Kak transformirovanie kopii mnozhestva vseh TNT-teorem (kazhdaya teorema otricaetsya)
No TNT (trinitrotoluol? A. S.) eti nadezhdy razneset v kloch'ya, potomu chto:
    (1) Vnutri mnozhestva vseh ne-teorem najdutsya nekotorye istinnye.*
    (2) Za predelami mnozhestva vseh invertirovannyh teorem najdutsya nekotorye lozhnye **

Vy uvidite, pochemu i kak eto sluchilos' v glave XIV. No poka obdumajte situaciyu po shematicheskomu obrazu predstavlennomu na ris. 18.

* Put' nekij dzhin bezostanovochno proizvodit vse teoremy TNT-teorii i tol'ko ih. No iz Teoremy Gedelya izvestno, chto v chisle teh cepochek, kotorye nikogda ne vydast TNT- dzhin est' cepochki, kotorye dejstvitel'no govoryat pravdu o chislah. Dzhin, konechno, mozhet beskonca lovit' nh i zastavlyat' na sebya rabotat' (to est' ob®yavit ih novymi aksiomami i iz nih stroit' teoremy teper' rasshirennoj TNT) No vsegda ostanutsya "vol'nye" istiny. Skol'ko ne lovi, vsegda budet ne ohvachennaya TNT-dzhinom pravda o chislah. Prim A. S.

** Puskaj TNT- dzhin mehanicheski vydaet vse istinnye cepochki TNT. A ego slugi bystren'ko "perekrashivayut" ih v "chernyj cvet" i sazhayut v tyur'mu (za to chto oni lgut). Krasyat oni tak: v nachalo kazhdoj cepochki pripisyvayut simvol otricaniya  (etot simvol est' v alfavite TNT).  V rezul'tate poluchaetsya mnozhestvo zavedomo lozhnyh cepochek. Odnako ne vse, dejstvitel'no lozhnye utverzhdeniya o chislah okazhutsya "za reshetkoj"  etogo  mnozhestva.  CHast'  lozhnyh  vsegda budet  gulyat' na svobode! Prim A. S.

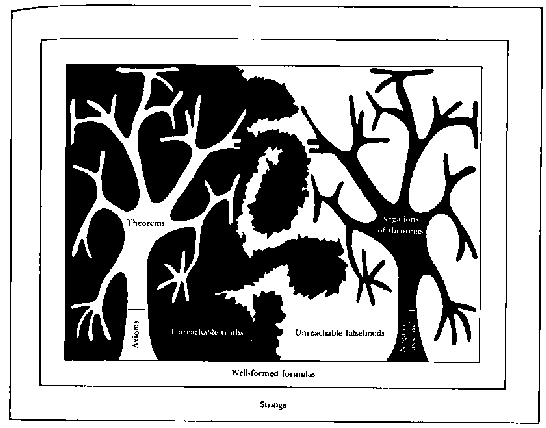
FIGURA 18. Zdes' vizual'no, v simvolicheskoj forme, pokazano otnoshenie mezhdu razlichnymi klassami cepochek TNT. Samaya bol'shaya ramka predstavlyaet mnozhestvo vseh cepochek sostavlennyh iz alfavita TNT. Sleduyushchaya vlozhennaya v nee ramka - mnozhestvo vseh pravil'no postroennyh cepochek TNT. V predelah etogo prostranstva i nahoditsya mnozhestvo vseh vyskazyvanij TNT. Teper' nachinaetsya samoe interesnoe. Mnozhestvo teorem izobrazheno kak krona dereva, rastushchaya iz stvola (predstavlyayushchego nabor aksiom). Derevo kak simvol bylo vybrano iz-za shodstva processa rosta s rekursiej, kotorym voznikayut novye teoremy: novye vetvi (teoremy), postoyanno vyrastayut ih staryh. Otpochkovyvayushchiesya rostki dereva pronikayut vo vse ugolki ogranichennogo ramkoj prostranstva, formiruya tem samym mnozhestvo istin, no ne mogut zapolnit' prostranstvo polnost'yu. Granica mezhdu mnozhestvom istin i mnozhestvom lozhnyh utverzhdenij, kak predpolagaetsya, predstavlyaet soboj beskonechno vetvyashchijsya fraktal, kotoryj, nezavisimo ot togo, kak gluboko vy issleduete ego, vsegda imeet bolee tonkie urovni vetvleniya i izloma, sledovatel'no, granicu nevozmozhno tochno opredelit' lyubym konechnym sposobom (Sm. knigu Mandelbrota "Fraktaly".) Zerkal'noe derevo predstavlyaet mnozhestvo otricatel'nyh teorem. Vse oni lozhnye, no ego vetvi vse zhe nesposobny ohvatit' vse lozhnye vyskazyvaniya. Oni ne ohvatyvayut vse prostranstvo lozhnyh utverzhdenij. [Risunok avtora.]

Figura i fon v muzyke

Mozhno tak zhe najti figuru i fon v muzyke. Odin primer - razlichie mezhdu melodiej i soprovozhdeniem. K melodii vsegda prikovano nashe vnimaniya, a soprovozhdenie v nekotorom smysle ej tol'ko pomogaet. Poetomu my udivleny, kogda nahodim na zadnem plane partii osnovnuyu melodiyu. |to redko byvaet v pop-muzyke. Obychno o soprovozhdenii ne dumayut kak o perednem plane. No v muzyke barokko, osobenno v muzyke Baha, chasto razlichnye linii ispolneniya libo vystupayut vpered, libo otstupayut nazad, podobno figure i fonu postoyanno menyayutsya mestami. V etom smysli partitury Baha mozhno nazvat' "rekursivnymi".
Drugaya analogiya dihotomii figura-fon v muzyke - eto razdelenie muzyke na glavnuyu tonal'nost' i sinkopu. Esli vy budete schitaete tona kak "osnovnoj, pol-tona, tret'-tona, chetver'-tona" to obychno noty sootvetstvuyut poryadku tonal'nostej. No inogda melodiya byvaet prednamerenno sdvinuta na odnu tonal'nost', chtoby yavno ee vydelit'. |to proishodit, naprimer, v nekotoryh etyudah dlya fortepiano SHopena. Takoj zhe priem shiroko ispol'zuetsya Bahom. Osobenno v ego sonatah dlya nesoprovozhdaemoj skripki, a takzhe v partii dlya nesoprovozhdaemoj violoncheli. Zdes' Bah uhitryaetsya poluchit' dve ili bolee linii zvuchaniya, idushchie odnovremenno. Inogda on (eto pri nalichii tol'ko soliruyushchego instrumenta) ispol'zuet tak skazat' "dvojnye akkordy" - dve noty neposredstvenno. Odnako, v drugih sluchayah on vstavlyaet odin golos v melodiyu, a drugoj v soprovozhdenie tak, chto my slyshim ih kak dve razlichnye melodii, perepletayushchiesya i garmoniruyushchie drug s drugom. Samo soboj razumeetsya, Bah ne ostanavlivaetsya na etom urovne slozhnosti. . . *

* K sozhaleniyu, "perevod" etogo razdela - pochti polnejshaya galimat'ya. Esli vy razbiraetes' v muzykal'noj teorii, to srazu eto pojmete. Esli net, to vam mozhet pokazat'sya, chto zdes' skryt smysl, kotoryj prosto nedostupen. No eto- illyuziya. Smysl original'nogo teksta dlya menya tozhe ostalsya neyasen. Poetomu ya soedinil slova bez osobogo bespokojstva o soderzhanii. Glavnoe - chtoby krasivo zvuchalo. Esli vy popalis' na etu ulovku, to, vozmozhno, uteshites' sleduyushchim nablyudeniem. Poluchilos', chto obychno "soliruyushchij" smysl pochti ischez, no horosho prorisovannyj "fon" ubedil vas v sushchestvovanii nekoj glubokomyslennoj "figury" Podobye illyuzii ne redko vstrechayutsya v zhizni. Osobenno - v politike. . . Prim A. S.

Rekursivno-schetnye mnozhestva i rekursivnye mnozhestva

Teper' pozvol'te ponyatie figury i fona perenesti obratno v oblast' formal'nyh sistem. V nashem primere rol' pozitivnogo prostranstva sygrali teoremy C-tipa, a rol' otricatel'nogo prostranstva sygrali cepochki s prostym chislom defisov. Poka edinstvennyj put', kotoryj my nashli, chtoby predstavit' prostye chisla tipografskim sposobom - predstavit' ih kak negativnoe prostranstvo. No imeetsya li( ne zavisimo ot togo naskol'ko eto slozhno) sposob predstavit' prostye chisla kak pozitivnoe prostranstvo? To est' mozhno li najti vse prostye chisla, kak mnozhestvo teorem nekotoroj formal'noj sistemy?

U raznyh lyudej raznaya intuiciya i oni podskazyvaet im razlichnye otvety. YA ochen' yarko pomnyu, kak byl udivlen i ozadachen posle togo, kak ponyal raznicu mezhdu pozitivnym i negativnym opisaniem. YA byl ves'ma ubezhden, chto ne tol'ko prostye chisla, no i lyuboe mnozhestvo chisel, kotoroe mozhno predstavleny kak negativ, vsegda mozhno predstavit' i kak pozitiv. Intuiciya, lezhashchaya v osnove moej very vyrazhaetsya voprosom: "Kak mogut figura i fon ne nesti odnu i tu zhe informaciyu?" Oni, kazalos' mne, voploshchayut tu zhe samuyu informaciyu, tol'ko zakodirovannuyu dvumya dopolnyayushchimi drug druga sposobami. Vy s etim soglasny?

Okazyvaetsya, ya byl prav po povodu prostyh chisel, no byl ne prav voobshche. |to udivilo menya i prodolzhaet udivlyat' dazhe segodnya. No fakt, chto:

    Sushchestvuyut formal'nye sistemy, ch'e otricatel'no prostranstv (mnozhestvo ne-teorem) ne yavlyaetsya pozitivnym prostranstvom (mnozhestvom teorem) kakoj-libo formal'noj sistemy.

|tot rezul'tat, okazyvaetsya, imeet tu zhe glubinu, chto i Teorema Gedelya. Poetomu ne udivitel'no, chto moya intuiciya zdes' ne srabotala. YA, tak zhe kak i matematiki nachala XX veka, ozhidal ot mir formal'nyh sistem i natural'nye chisla bol'shej predskazuemosti. Govorya tehnicheskim yazykom, poluchaetsya:

    Sushchestvuyut rekursivno-schetnye mnozhestva, kotorye ne rekursivny.

Slovosochetanie rekursivno-schetnyj (chast' sokrashchaemoe do "r.e.") - matematicheskij bliznec nashemu ponyatiyu "kursivno prorisovannyj", a ponyatie rekursivnyj - bliznec "rekursivno prorisovannyj". Dlya nekotorogo mnozhestva cepochek, byt' "r.e", oznachaet, chto ono mozhet byt' polucheno soglasno tipografskim pravilam. Takovo, naprimer, mnozhestvo teorem C-tipa i mnozhestvo teorem MIU-sistemy. V dejstvitel'nosti rekursivno-schetnym budet mnozhestvo teorem lyuboj formal'noj sistemy. |to mozhno predstavit' po analogii ideej "figury" kak "mnozhestvo linij, kotorye mozhno postroit' po zakonam izobrazitel'nogo iskusstva" (i ne vazhno, chto eti linii mogut oznachat'!). Rekursivnoe zhe mnozhestvo podobno toj figure, chej fon - tozhe figura. To est' rekursivnoe mnozhestvo ne tol'ko "r.e." no i ego dopolnenie tozhe "r.e." *

* Zdes' nasha intuiciya igraet s nami zluyu shutku. Predstav'te sebe troglika, kotoryj varklivo-chuvatyj. Teper' predstav'te troglika chuvatogo. YAvlyaetsya li vsyakij vakrvivo-chuvatyj troglik odnovremenno i chuvatym? Estestvenno dumat', chto oba troglika varkliy no odin iz nih eshche i chuvatyj. To est' varklivo-chuvatye troglichi est' raznovidnost' varklivyh troglikov voobshche. No vy oshiblis' tak zhe kak, s rekursivno-schetnymi i "prosto" rekursivnymi mnozhestvami. Vse naoborot! Varklivo-chuvatyj ne obyazatel'no varklivyj. Varklivye est' raznovidnost'( podmnozhestvo) varklivo-chuvatyh! Pochemu? U troglikov tak prinyato. I ves' tut skaz! Prim. A. S.

Iz vysheupomyanutogo rezul'tata sleduet:

    Sushchestvuyut formal'nye sistemy, dlya kotoryh ne sushchestvuet nikakoj razreshayushchej procedury realizuemoj tipografskim sposobom.

Iz chego eto sleduet? Ochen' prosto. Tipografskaya razreshayushchaya procedura - eto metod, kotoryj otlichaet teoremy ot ne-teorem. Sushchestvovanie takogo testa pozvolyaet nam posledovatel'no proizvodit' vse ne-teoremy. Dlya etogo, dvigayas' po spisku vseh cepochek, vy kazhduyu ispytyvaete razreshayushchej proceduroj. Po rezul'tatu vy otbrakovyvaete ploho formalizovannye cepochki i teoremy, ostavlyaya odni ne-teoremy. Opisannaya procedura sootvetstvuet tipografskomu metodu polucheniya mnozhestva ne-teorem. No soglasno bolee rannemu utverzhdeniyu (kotoroe my zdes' prinyali na veru), dlya nekotoryh sistem eto nevozmozhno. Poetomu, priznav ego, my vynuzhdeny zaklyuchit', chto i tipografskie razreshayushchie procedury sushchestvuyut ne dlya vseh formal'nyh sistem.

Predpolozhim, chto my nashli mnozhestvo natural'nyh chisel F, ('F'- ang. "figury"), kotoroe my mozhem proizvesti nekotorym formal'nym sposobom, na podobii mnozhestva sostavnyh chisel. Predpolozhim, chto ego dopolnenie - mnozhestvo G ('G'- angl. "osnovanie", fon), na podobii prostyh chisel. Vmeste mnozhestva F i G sostavlyayut mnozhestvo natural'nyh chisel. My znaem pravilo, po kotoromu my mozhem poluchit' vse chisla mnozhestva F. No my ne znaem nikakogo podobnogo pravila dlya polucheniya vseh chisel mnozhestva G. Vazhno ponyat', chto esli chleny mnozhestva F vsegda proizvodyatsya v poryadke uvelicheniya razmera, to my vsegda mozhem vydelit' i G kak negativ. No problema v tom, chto mnogie "r.e." mnozhestva perechislyayutsya metodami, kotorye vydayut svoi elementy v proizvol'nom poryadke. Poetomu vy nikogda ne znaete, budet li chislo, kotoroe vy tol'ko chto pereskochili, polucheno kogda-nibud' v budushchem ili net, esli vy podozhdite process kakoe-to vremya eshche.*

* tochno vyyasnit' eto mozhno tol'ko za beskonechnyj promezhutok vremeni, no takaya situaciya nam uzhe nepriyatno znakoma. Prim. A. S.

My otvetili "net" na vopros: "yavlyayutsya i vse figury rekursivnymi?" My teper' vidim, chto analogichno dolzhny otvetit' i na podobnyj vopros v matematike: "YAvlyayutsya li vse mnozhestva rekursivnymi?" S etoj tochki zreniya davajte teper' vernut'sya k neulovimomu terminu "forma". Pozvol'te vzyat' nashe mnozhestvo-formu F i mnozhestvo-foru G. My mozhem soglasit'sya chto vse chisla v mnozhestve F imeyut nekotoruyu obshchuyu "formu". No mozhno li tozhe skazat' otnositel'no chisel mnozhestva G? |to strannyj vopros. Kogda my imeem delo s beskonechnymi mnozhestvami, naprimer s natural'nymi chislami, to "dyry" sozdannye udaleniem nekotorogo podmnozhestva, ochen' trudno opredelit' nekotorym yavnym sposobom. I mozhet sluchit'sya tak, chto oni ne svyazany drug s drugom nikakim obshchim priznakom ili "formoj" voobshche. V poslednem sluchae vopros vkusa hotite li vy dlya takogo ponyatiya ispol'zovat' termin "forma" ili net, no razmyshlyat' o nem kak o nekoj forme - provokaciya. Byt' mozhet luchshe ne opredelyat' "formu" tverdo, a ostavit' ee plastichnoj.*

* Davajte opredelim formu kak kontur, kotoryj smelo mozhno zakrasit' nekotorym cvetom. Pozitivnye elementy odnoznachno imeyut formu. Po mere ih obnaruzheniya (perechisleniya) my "obvodim" ih konturom i smelo zakrashivaem belym cvetom. No kak postupat' s negatiom?! Esli my znaem, chto bol'she nikogda ne vernemsya tuda, gde tol'ko chto pokrasili VSE belye formy, to mozhno smelo zakrashivat' chernym i promezhutki mezhdu nimi. Negativ tozhe priobretaet formu (imenno priobretaet, process beskonechen, no v lyuboj moment my imeem "zatverdevshuyu" chast' formy, ne podlezhashchuyu peredelke). A esli uverennosti net? Esli v promezhutke est' poka eshche neizvestnyj pozitiv? A my ego zakrasim chernym?!. . . Znachit, k zakraske chernyh promezhutkov (polucheniyu negativnoj formy) my smozhem pristupit' tol'ko, kogda opredelim VSE belye formy. To est' spustya beskonechnost'. . . Prim. A.S,

Imeetsya golovolomka, dlya razmyshleniya nad vysheizlozhennymi voprosami. Vy mozhete harakterizovat' sleduyushchuyu posledovatel'nost' chisel (ili ih otricatel'noe prostranstvo)?

1      3       7       12       18       26       35       45       56       69       .   .   .

CHem eta posledovatel'nost' napominaet figurno-figurnuyu figuru?

Prostye chisla: prostupayut kak figura, a ne fon

V konce koncov, chto s formal'noj sistemoj dlya prostyh chisel? Kak ee postroit'? Nasha ulovka dolzhna obojti umnozhenie i pryamo pereskochit' k nedelimosti, kak pozitivno predstavlennoj sushchnosti. Imeyutsya shema aksiom i pravilo vyvoda dlya sozdaniya teorem, kotorye vyrazhayut predstavlenie, chto odno chislo ne delit ('DND' - 'does not divide') drugoe chislo.

    Shema aksiom: xyDNDx, gde h i u - raznye cepochki defisov (X ne ravno Y).
Naprimer _ _ _ _ _ DND _ _ gde x zamenen na '_ _' , a u na ' _ _ _ '

    Pravilo: Esli xDNDu - teorema, to teorema i xDNDxy.
Esli vy ispol'zuete eto pravilo dvazhdy k privedennoj vyshe aksiome, to poluchite takuyu teoremu: _ _ _ _ _ DND _ _ _ _ _ _ _ _ _ _ _ _

Kotoraya interpretiruetsya, kak "5 ne delit 12". No _ _ _ DND _ _ _ _ _ _ ne teorema. CHto proishodit ne tak, kak nado, esli vy poprobuete poluchit' ee?

Teper' chtoby opredelit', chto dannoe chislo yavlyaetsya prostym, my dolzhny poluchit' nekotoroe znanie otnositel'no ego svojstva nedelimosti. V chastnosti my hotim znat', chto nekotoroe chislo ne delimo ni na 2, ni na 3, ni na 4 i t. d. vse do chisla men'shego na 1 chem ono samo. No my ne mozhem byt' stol' neopredelenny v formal'nyh sistemah, chtoby govorit' "i tak dalee". My dolzhny raz®yasnit' eto. My hoteli by imet' sposob vyskazat' na yazyke sistemy "chislo Z svobodno ot delitelej ne bol'shih X". chto oznachaet: nikakoe chislo ot 2 do H ne delit Z. |to mozhet byt' sdelano, no nuzhna ulovka. Podumajte ob etom, esli hotite. Vot eto reshenie:

    Pravilo: esli _ _ DNDz est' teorema, to i zDF_ _ tozhe teorema.
    Pravilo: esli zDFx teorema, i x _ DNDz tozhe teorema, to i zDFx _ teorema.

|ti dva pravila ohvatyvayut ponyatie nedelimosti. Vse chto my teper' dolzhny delat', eto skazat', chto prostoe chislo eto takoe, kotorye nedelimy na chislo, men'shie na 1 chem ono samo:

    Pravilo: Esli z_DFz teorema, to Rz _ tozhe teorema.
Da! ne stoit zabyvat' chto 2 - prostoe chislo!

    Aksioma: P_ _

I tak my poluchili vse chto hoteli. Formal'noe predstavlenie prostyh chisel. Imet'sya ispytanie na nedelimost', kotoroe mozhet byt' sdelano bez kakogo-libo otslezhivaniya nazad. Vy mozhete uverenno dvigat'sya vverh, proveryaya snachala nedelimost' na 2, zatem na 3 i tak dalee. |to "monotonnyj" ili "odnonapravlennyj" process. Zdes' net neobhodimosti vo vzaimnoj igre udlinenie-sokrashchenie. Nam net nuzhdy v poperemennom uvelichenii i umen'shenii dlinny cepochek dlya togo, chtoby vysledit' vse prostye chisla. No u formal'nyh sistem est' i takaya vozmozhnost'. I imenno eta potencial'naya vozmozhnost' formal'nyh sistem nepredskazuemo peremeshivat' predydushchee s posleduyushchim, v itoge vlechet takie ogranichivayushchie rezul'taty kak Teorema Gedelya, Problema Ostanovki T'yuringa i tot fakt, chto ne vse rekursivno-schetnye mnozhestva rekursivny.

[ predydushchaya ] [ oglavlenie ] [ sleduyushchaya ]
Sopyleft © A Semenov 2002
[ vverh ]